b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
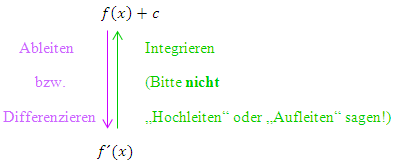
Nun wird das Ganze noch etwas komplizierter. Stelle dir vor, dass es oberhalb von 
noch eine weitere Funktion 
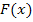gibt, deren Ableitung 
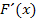die Funktion ergibt. So eine Funktion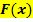 
heißt Stammfunktion von 
.
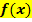Es gilt demnach für eine Stammfunktion :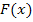
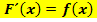
Mit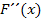 
– sprich:„F zwei Strich von x“ – ist die zweite Ableitung von 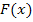gemeint. Die zweite Ableitung haben wir eigentlich noch gar nicht eingeführt. Merke dir einfach, dass man eine Funktion im Prinzip beliebig oft ableiten kann. Um die zweite Ableitung zu erhalten, leitet man einfach die erste Ableitung noch einmal ab. Leitet man die zweite Ableitung wieder ab, erhält man die dritte Ableitung usw. An dieser Stelle soll uns das genügen. Was die höheren Ableitungen einer Funktion anschaulich bedeuten, musst du im Moment noch nicht wissen. (Mehr dazu erst bei Zweite Ableitung 
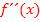und bei Wendepunkte mit der dritten Ableitung nachweisen) Aber Vorsicht:Mit 
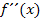ist die zweite Ableitung von gemeint, was wiederum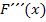 
entspricht. Doch damit werden wir uns erst später genauer beschäftigen.
Die jeweils untere Funktion stellt immer die Ableitung der direkt darüber stehenden Funktion dar;ihr Funktionswert entspricht jeweils der Steigung der direkt darüber liegenden Funktion.
Der Begriff der Stammfunktion wird im Kapitel Einführung in die Integralrechnung noch ausführlicher besprochen. Im Moment reicht es für dich aus zu wissen, dass eine Funktion 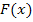Stammfunktion zu ist, wenn für ihre Ableitung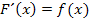 
gilt. Nun aber wieder zurück zum Zusammenhang von und 
.
Für den Fall, dass dir das alles noch nicht so ganz klar ist, schauen wir uns jetzt ein paar konkrete Beispiele an. Daran werden die oben beschriebenen Zusammenhänge vertieft dargestellt.
1. Bsp.:
Gegeben sind die Funktionen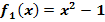 
, 
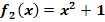und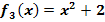 
. Bilde jeweils die Ableitung mit Hilfe der Ableitungsregeln! Was fällt dir dabei auf? Zeichne die Graphen dieser drei Funktionen und ihre Ableitungsfunktion in ein gemeinsames Koordinatensystem!
Lösung:
Laut Ableitungsregel gilt: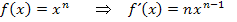 
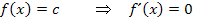
Mit dieser Regel erhalten wir die Ableitungen der gegebenen drei Funktionen.
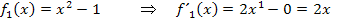
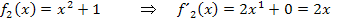
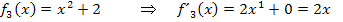
Offensichtlich haben alle drei Funktionen die gleiche Ableitung, da sich die Funktionsgleichungen ja nur in ihren additiven Konstanten unterscheiden.
Nun zeichnen wir die Graphen der drei Funktionen mit ihrer gemeinsamen Ableitungsfunktion in ein gemeinsames Koordinatensystem. Das dürfte ja kein Problem für dich darstellen. Alle drei Funktionen stellen schließlich jeweils nach oben geöffnete Normalparabeln dar, die sich allerdings in ihren Scheitelpunkten unterscheiden. Die erste hat ihren Scheitel bei (0|-1), die zweite bei (0|1) und die dritte bei (0|2). Die Graphen haben also alle die gleiche Form, sie sind nur mehr oder weniger nach oben/unten verschoben. Die gemeinsame Ableitungsfunktion ist eine Gerade durch den Ursprung mit der Steigung m = 2.
