b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Andere Lehrer(innen) stellen das Steigungsverhalten nicht in Tabellenform dar, sondern in folgender Art und Weise:
für 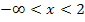 :
: 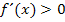

 streng monoton steigend
streng monoton steigend
für 2 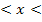 4:
4: 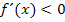

 streng monoton fallend
streng monoton fallend
für 4 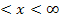 :
: 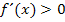

 streng monoton steigend
streng monoton steigend
In dieser Form lässt sich jedoch nicht so gut erkennen, welche Art von Extremum vorliegt, also ob es sich bei dem Punkt mit waagrechter Tangente jeweils um einen Tiefpunkt oder um einen Hochpunkt handelt. Daher ist an sich die Monotonietabelle zu bevorzugen.
Bevor die Monotonietabelle angelegt werden kann, müssen jedoch zuerst die x-Koordinaten der Punkte mit waagrechten Tangenten ermittelt werden. (In der oben im letzten Beispiel dargestellten Monotonietabelle x = 2 und x = 4) Das macht man mit dem Ansatz 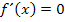 , da die Steigung
, da die Steigung  der Funktion gleich der Tangentensteigung in diesem Punkt, also gleich Null sein muss. Zur Berechnung der Steigung einer Funktion
der Funktion gleich der Tangentensteigung in diesem Punkt, also gleich Null sein muss. Zur Berechnung der Steigung einer Funktion  benötigt man daher die erste Ableitung
benötigt man daher die erste Ableitung  .
.
Mit Hilfe des Steigungsverhaltens, d.h. der Monotonie, kann leicht unterschieden werden, ob ein Extremum oder Terrassenpunkt vorliegt. Nur bei einem Vorzeichenwechsel von  liegt ein Extremum vor.
liegt ein Extremum vor.
| Zusammenfassung:
Verlauf der Ableitungsfunktion
Nullstelle mit Vorzeichenwechsel von Nullstelle ohne Vorzeichenwechsel von |
Im Prinzip gibt es zwei verschiedene Aufgabenstellungen zum Zusammenhang zwischen  und
und  . Entweder ist
. Entweder ist  gegeben und es soll der Graph der Ableitungsfunktion
gegeben und es soll der Graph der Ableitungsfunktion  skizziert werden, oder der Graph der Ableitungsfunktion
skizziert werden, oder der Graph der Ableitungsfunktion  ist gegeben und man soll Aussagen über den Verlauf von
ist gegeben und man soll Aussagen über den Verlauf von  machen. Bei manchen Aufgaben muss auch verschiedenen Ableitungsgraphen ein jeweils zugehöriger Funktionsgraph zugeordnet werden.
machen. Bei manchen Aufgaben muss auch verschiedenen Ableitungsgraphen ein jeweils zugehöriger Funktionsgraph zugeordnet werden.
Vom Funktionsgraph 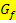 lässt sich eindeutig auf die Ableitungsfunktion schließen, jedoch nicht umgekehrt. Ist nur die Ableitung bekannt, kann man nämlich nur eindeutige Aussagen zum Steigungsverhalten der Funktion
lässt sich eindeutig auf die Ableitungsfunktion schließen, jedoch nicht umgekehrt. Ist nur die Ableitung bekannt, kann man nämlich nur eindeutige Aussagen zum Steigungsverhalten der Funktion  machen, aber man kann nicht auf die y-Koordinaten der Kurvenpunkte von
machen, aber man kann nicht auf die y-Koordinaten der Kurvenpunkte von  kommen.
kommen.
Im Kapitel Einfache Ableitungsregeln wurde schon im 4. Bsp. darauf eingegangen, dass es nicht möglich ist von  eindeutig auf
eindeutig auf  zu schließen. Beim Ableiten fallen additive Konstanten bekanntlich weg. Daher kann eine bestimmte Ableitung
zu schließen. Beim Ableiten fallen additive Konstanten bekanntlich weg. Daher kann eine bestimmte Ableitung  von verschiedenen Funktionen kommen. Diese Funktionen unterscheiden sich allerdings nur in ihrer additiven Konstante. (Ihre Funktionsgraphen sind nur nach oben oder unten verschoben.) Das Berechnen von
von verschiedenen Funktionen kommen. Diese Funktionen unterscheiden sich allerdings nur in ihrer additiven Konstante. (Ihre Funktionsgraphen sind nur nach oben oder unten verschoben.) Das Berechnen von  ausgehend von
ausgehend von  nennt man übrigens integrieren. (Bitte nicht „hochleiten“ oder „aufleiten“ sagen!) Auf die Konstante c kann man beim Integrieren nur dann kommen, wenn man eine weitere Information über
nennt man übrigens integrieren. (Bitte nicht „hochleiten“ oder „aufleiten“ sagen!) Auf die Konstante c kann man beim Integrieren nur dann kommen, wenn man eine weitere Information über  hat, beispielsweise die Koordinaten eines Kurvenpunktes von
hat, beispielsweise die Koordinaten eines Kurvenpunktes von  .
.