b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
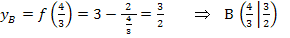
Nun fehlt nur noch die Tangentengleichung. In Abhängigkeit von 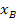 haben wir sie bereits ermittelt:
haben wir sie bereits ermittelt: 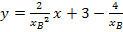
In diese Gleichung setzen wir 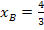 ein und vereinfachen soweit möglich.
ein und vereinfachen soweit möglich.
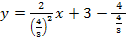
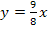
Dies ist die Gleichung der Tangente an die Funktion 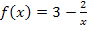 , die durch den Ursprung verläuft. Der Berührpunkt ist
, die durch den Ursprung verläuft. Der Berührpunkt ist 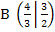 .
.
Hinweis:Zur Kontrolle der Rechnung kann hier die Tatsache verwendet werden, dass der y-Achsenabschnitt t der ermittelten Tangente wirklich gleich Null ist. Aus 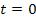 folgt, dass die Tangente tatsächlich durch den Ursprung verläuft, wie in der Aufgabenstellung verlangt.
folgt, dass die Tangente tatsächlich durch den Ursprung verläuft, wie in der Aufgabenstellung verlangt.
Zusammenfassung:
Es gibt zwei unterschiedliche Aufgabentypen rund um das Thema „Tangentengleichung aufstellen“. Beim einfacheren Typ ist der Berührpunkt, also ein Punkt der Funktion  angegeben, in dem die Tangente an
angegeben, in dem die Tangente an  gelegt werden soll. Beim schwierigeren Typ ist dagegen nur ein Punkt P der Tangente gegeben, der aber nicht auf
gelegt werden soll. Beim schwierigeren Typ ist dagegen nur ein Punkt P der Tangente gegeben, der aber nicht auf  liegt. Von diesem Punkt P ausgehend soll(en) die Tangente(n) an
liegt. Von diesem Punkt P ausgehend soll(en) die Tangente(n) an  gelegt werden. Wenn du die Gleichung einer Tangente aufstellen sollst, musst du die beiden unterschiedlichen Aufgabenstellungen genau unterscheiden. Beim schwierigeren Typ bei dem ein Punkt gegeben ist, der nicht auf
gelegt werden. Wenn du die Gleichung einer Tangente aufstellen sollst, musst du die beiden unterschiedlichen Aufgabenstellungen genau unterscheiden. Beim schwierigeren Typ bei dem ein Punkt gegeben ist, der nicht auf  liegt, können eventuell auch mehrere Lösungen herauskommen. Das hängt von der gegebenen Funktion und vom Punkt ab.
liegt, können eventuell auch mehrere Lösungen herauskommen. Das hängt von der gegebenen Funktion und vom Punkt ab.
Eine Anleitung für den einfacheren Typ hast du bereits weiter oben erhalten. Zum Schluss noch die Anleitung für den schwierigeren Typ in Stichworten.
Geg.: Funktionsgleichung 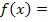 … und Punkt … und Punkt 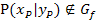
„Schwierigeres Tangentenproblem“ Ges.: Tangentengleichung an · y-Koordinate von B (in Abhängigkeit von d.h. · · Tangentensteigung m (in Abhängigkeit von d.h. · y-Achsenabschnitt t (in Abhängigkeit von · Tangentengleichung (in Abhängigkeit von · Den gegebenen Punkt
· y-Koordinate von B berechnen: d.h. den berechneten Wert · Tangentengleichung aufstellen:Den berechneten Wert |

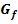 von P ausgehend
von P ausgehend  und Berührpunkt
und Berührpunkt 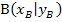
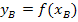


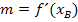
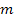 einsetzen in
einsetzen in 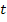 einsetzen in
einsetzen in 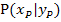 für x bzw. y in die soeben aufgestellte Tangentengleichung einsetzen und nach
für x bzw. y in die soeben aufgestellte Tangentengleichung einsetzen und nach 