b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Zur Verdeutlichung der unterschiedlichen Tangentenprobleme hier zwei Abbildungen:
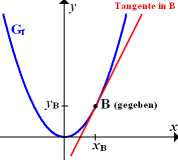
| „Einfacheres Tangentenproblem“
Im Kurvenpunkt
|
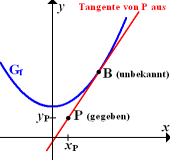
„Schwierigeres Tangentenproblem“
Von einem Punkt
|
Wie kann man nun von einem Punkt P außerhalb von  die Tangente an
die Tangente an  legen?
legen?
Wir rechnen erst einmal so, als würden wir die x-Koordinate 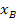 des Berührpunktes
des Berührpunktes 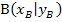 kennen. Mathematisch gesagt, wir rechnen zu Beginn in Abhängigkeit von
kennen. Mathematisch gesagt, wir rechnen zu Beginn in Abhängigkeit von 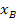 . („In Abhängigkeit von
. („In Abhängigkeit von 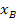 rechnen“ bedeutet, dass man mit
rechnen“ bedeutet, dass man mit 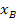 rechnet als wäre es eine bekannte Zahl;man setzt allerdings nichts für
rechnet als wäre es eine bekannte Zahl;man setzt allerdings nichts für 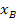 ein.) Wir tun praktisch so, als wäre
ein.) Wir tun praktisch so, als wäre 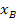 eine konkrete Zahl und stellen die Gleichung der Tangente erst einmal in Abhängigkeit von
eine konkrete Zahl und stellen die Gleichung der Tangente erst einmal in Abhängigkeit von 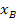 auf. Dann setzten wir die Koordinaten des gegebenen Punktes, in diesem Fall P(0|0), in die Tangentengleichung ein und lösen nach
auf. Dann setzten wir die Koordinaten des gegebenen Punktes, in diesem Fall P(0|0), in die Tangentengleichung ein und lösen nach 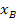 auf. So ergibt sich die x-Koordinate des Berührpunktes. Damit ist unsere Aufgabe schon fast gelöst. Die noch fehlende y-Koordinate von B und die Tangentengleichung lassen sich dann ja leicht berechnen. (Genaueres siehe unten!)
auf. So ergibt sich die x-Koordinate des Berührpunktes. Damit ist unsere Aufgabe schon fast gelöst. Die noch fehlende y-Koordinate von B und die Tangentengleichung lassen sich dann ja leicht berechnen. (Genaueres siehe unten!)
So, jetzt geht´s los. Wir gehen Schritt für Schritt vor, im Prinzip wie bei der Berechnung der Tangente, wenn der Berührpunkt 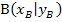 gegeben ist, nur dass wir für
gegeben ist, nur dass wir für 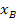 erst mal nichts einsetzen, da wir
erst mal nichts einsetzen, da wir 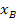 ja noch nicht kennen.
ja noch nicht kennen.
Hier noch einmal die Funktionsgleichung: 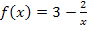
Gesuchter Berührpunkt 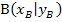
· y-Koordinate von B berechnen: 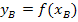
d.h. 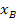 in
in  einsetzen
einsetzen
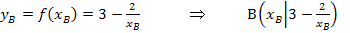
·  ableiten
ableiten 

Um die Funktion 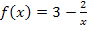 besser ableiten zu können, formen wir sie mit Hilfe des Potenzgesetzes
besser ableiten zu können, formen wir sie mit Hilfe des Potenzgesetzes  um.
um.
Dann kann nämlich mit Hilfe der Ableitungsregel 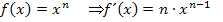 abgeleitet werden.
abgeleitet werden.

· Tangentensteigung m (in Abhängigkeit von 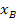 ) berechnen:
) berechnen: 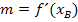
d.h. 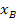 in
in  einsetzen
einsetzen
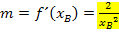
· y-Achsenabschnitt t (in Abhängigkeit von 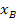 ) berechnen: Dazu die Koordinaten von
) berechnen: Dazu die Koordinaten von 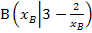 für x bzw. y sowie berechneten Wert
für x bzw. y sowie berechneten Wert 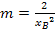 in
in  einsetzen und nach t auflösen
einsetzen und nach t auflösen

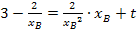
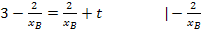
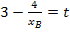
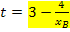
· Tangentengleichung (in Abhängigkeit von 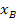 ) aufstellen: Nur die soeben berechneten Werte
) aufstellen: Nur die soeben berechneten Werte 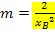 und
und 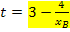 einsetzen in
einsetzen in  (Für x und y nichts einsetzen!)
(Für x und y nichts einsetzen!)
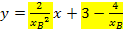 (Tangentengleichung in Abhängigkeit von
(Tangentengleichung in Abhängigkeit von 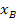 )
)
Die Tangente soll laut Angabe durch den Ursprung (0|0) verlaufen. Der Ursprung muss daher auf der Tangente liegen;die Gleichung muss für seine Koordinaten erfüllt sein. Wir können den Punkt (0|0) somit in die Tangentengleichung einsetzen und dann nach 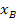 auflösen.
auflösen.
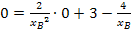



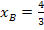
Jetzt kennen wir die x-Koordinate des Berührpunktes B. Die y-Koordinate 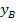 muss noch berechnet werden. Dazu setzten wir die x-Koordinate
muss noch berechnet werden. Dazu setzten wir die x-Koordinate 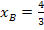 einfach in
einfach in 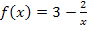 ein.
ein.

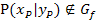 die Tangente(n) an
die Tangente(n) an