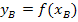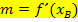b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
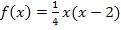
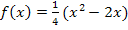
Jetzt leiten wir mit der Regel 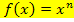 mit n
mit n  ℝ
ℝ 
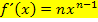 ab. Das ergibt:
ab. Das ergibt:
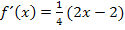
Wir klammern noch die Zahl 2 aus. (Das muss man nicht unbedingt machen;man könnte genauso gut 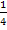 in die Klammer hineinmultiplizieren.) Dadurch erhält man:
in die Klammer hineinmultiplizieren.) Dadurch erhält man:
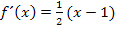
Nun bilden wir 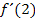 , also die Ableitung an der Stelle
, also die Ableitung an der Stelle 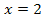 . Dazu setzt man einfach die Zahl 2 für x in die Ableitung (genauer gesagt:in die Ableitungsfunktion)
. Dazu setzt man einfach die Zahl 2 für x in die Ableitung (genauer gesagt:in die Ableitungsfunktion)  ein. Man erhält:
ein. Man erhält:
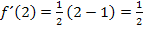
Nun müssen wir nur noch den Schnittwinkel der Tangente mit der x-Achse berechnen.
Wie schon im 5. Bsp. und 7. Bsp. verwenden wir die Formel:
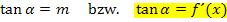
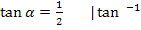
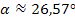
10. Bsp.:Schwierigeres Tangentenproblem
Vom Ursprung ausgehend wird an die Funktion 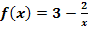 die Tangente gelegt. In welchem Punkt B berührt diese Tangente den Funktionsgraph? Wie lautet die Gleichung dieser Tangente?
die Tangente gelegt. In welchem Punkt B berührt diese Tangente den Funktionsgraph? Wie lautet die Gleichung dieser Tangente?
Lösung:
Diese Aufgabe hat es in sich. Das Problem besteht darin, dass man nicht weiß, wo die Tangente den Funktionsgraph  berührt. Genau der Berührpunkt
berührt. Genau der Berührpunkt 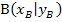 zwischen der Tangente und dem Funktionsgraphen ist in dieser Aufgabe nicht bekannt, sondern gesucht. Bisher war genau dieser Berührpunkt, oder zumindest seine x-Koordinate, immer angegeben, wenn eine Tangentengleichung gesucht war. Wir setzten die gegebene x-Koordinate
zwischen der Tangente und dem Funktionsgraphen ist in dieser Aufgabe nicht bekannt, sondern gesucht. Bisher war genau dieser Berührpunkt, oder zumindest seine x-Koordinate, immer angegeben, wenn eine Tangentengleichung gesucht war. Wir setzten die gegebene x-Koordinate 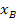 des Berührpunktes B in die Funktionsgleichung
des Berührpunktes B in die Funktionsgleichung  ein, falls seine y-Koordinate noch unbekannt war, und berechneten so seine y-Koordinate
ein, falls seine y-Koordinate noch unbekannt war, und berechneten so seine y-Koordinate 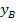 . Der Berührpunkt B liegt schließlich sowohl auf der Tangente als auch auf der Funktion
. Der Berührpunkt B liegt schließlich sowohl auf der Tangente als auch auf der Funktion  . Dann setzten wir seine x-Koordinate
. Dann setzten wir seine x-Koordinate 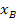 in die erste Ableitung
in die erste Ableitung  ein und erhielten die Steigung m der Tangente. durch Einsetzen von m und der Koordinaten von B in die allgemeine Geradengleichung
ein und erhielten die Steigung m der Tangente. durch Einsetzen von m und der Koordinaten von B in die allgemeine Geradengleichung  ließsich der y-Achsenabschnitt t der Tangente ermitteln.
ließsich der y-Achsenabschnitt t der Tangente ermitteln.
| Zur Wiederholung:
Anleitung zum Aufstellen der Tangentengleichung, wenn Berührpunkt gegeben „Einfacheres Tangentenproblem“ Geg.: Funktionsgleichung Ges.: Tangentengleichung an Anleitung: · Allgemeiner Ansatz: · y-Koordinate von B berechnen: d.h. x-Koordinate von B in · · Tangentensteigung m berechnen: d.h. x-Koordinate von B in · y-Achsenabschnitt t berechnen: Koordinaten von B für x bzw. y sowie berechneten Wert für m in · Tangentengleichung aufstellen: Nur die berechneten Werte für m und t einsetzen in |
In dieser Aufgabe ist aber statt des Berührpunktes B nur der Punkt P(0|0) gegeben, der zwar auf der Tangente, jedoch nicht auf der Funktion  liegt. Wir wissen also nicht, wo die Tangente die Funktion berührt. Wir brauchen aber den Berührpunkt B, um die Tangentengleichung aufstellen zu können. Ohne die Tangentengleichung kann umgekehrt der Berührpunkt nicht direkt ermittelt werden.
liegt. Wir wissen also nicht, wo die Tangente die Funktion berührt. Wir brauchen aber den Berührpunkt B, um die Tangentengleichung aufstellen zu können. Ohne die Tangentengleichung kann umgekehrt der Berührpunkt nicht direkt ermittelt werden.

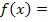 … und Berührpunkt
… und Berührpunkt 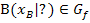
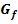 im Punkt B
im Punkt B