b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
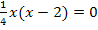
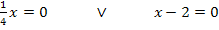
(Das mathematische Zeichen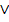 
bedeutet „oder auch“. Du kannst es auch weglassen und zum Beispiel stattdessen einen Strichpunkt verwenden.)
Nun müssen wir also die beiden einzelnen Gleichungen lösen. Eigentlich kann man die Lösungen sofort sehen.
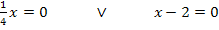
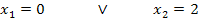
Nicht klar? Ok, dann machen wir das zusammen ganz langsam. Du überlegst dir folgendes:
Aus der Gleichung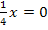 
folgt direkt: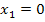 
Falls dir das nicht sofort einleuchtet, kannst du diese Gleichung „normal“ nach x auflösen, indem du durch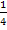 
dividierst bzw. mit dem Kehrwert 
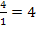multiplizierst. Aber Vorsicht:Null durch eine beliebige Zahl dividiert ergibt wieder Null! Entsprechend bei der Multiplikation:Null mit einer beliebigen Zahl multipliziert ergibt wieder Null! Warum das hier extra erwähnt wird? Du kannst dir gar nicht vorstellen, wie oft an dieser Stelle Fehler passieren! Also noch einmal ganz ausführlich:
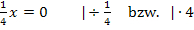
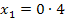
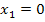
(Hier kommt also definitiv nicht die Zahl 1 oder 4 heraus! Auch wenn das viele Schüler denken. Also bitte Vorsicht an dieser Stelle! Bei zehn verschiedenen Schülern passiert hier tatsächlich neunmal ein Fehler.)
Jetzt zu der zweiten Gleichung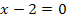 
. Die Lösung kann man sofort erkennen;man muss eigentlich nur die Zahl -2 auf die rechte Seite der Gleichung bringen. Es folgt:
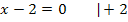
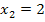
Die Funktion 
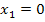hat also die zwei Nullstellen und .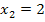
Wir interessieren uns nur für die positive Nullstelle, also für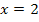 
.
Da wir den Schnittwinkel der Tangente bei 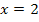mit der x-Achse suchen, müssen wir als nächstes die Tangentensteigung bei 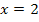berechnen, d.h. die Ableitung 
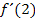. Dazu bilden wir erst die Ableitungsfunktion 
und setzen dann den Wert 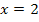ein. Den Schnittwinkel mit der x-Achse kann man dann mit der Formel 
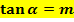berechnen, wobei m für die Steigung der Tangente steht, also hier für 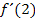. Das kannst du gleich ´mal selbst probieren.
Hier noch einmal die Funktionsgleichung: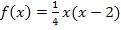 
Um abzuleiten, multipliziert man am besten x in die Klammer hinein. Den Faktor 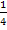kann man außerhalb der Klammer stehen lassen. Wie du weißt, bleiben multiplikative Konstanten (Zahlen ohne x, die mit irgendetwas anderem multipliziert werden) beim Ableiten einfach stehen. Das x solltest du aber auf jeden Fall vor dem Ableiten in die Klammer hineinmultiplizieren, denn ansonsten bräuchte man die sogenannte Produktregel. Dies ist eine weitere Ableitungsregel, die man immer bei Produkten braucht, wenn in beiden Faktoren x vorkommt. Die Produktregel wird ausführlich erläutert im Kapitel Weitere Ableitungsregeln. Im Moment wollen wir diese Regel aber noch nicht verwenden, weil wir sie noch gar nicht wirklich eingeführt haben. Das Ableiten unserer Funktion würde damit außerdem wesentlich länger dauern. Also besser x in die Klammer hineinmultiplizieren, bevor du ableitest!
