b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Die y-Koordinaten der beiden Extrema haben wir oben schon berechnet. Hier noch einmal die Ergebnisse:
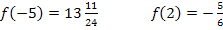
Damit können wir nun die Koordinaten des Hoch- und des Tiefpunktes angeben.
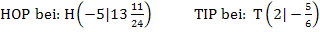
Fertig! Wir haben Art und Lage der Extrema von 
ermittelt.
Hinweis zur Benennung der Punkte:Ein Punkt wird mathematisch korrekt immer mit einem einzigen Großbuchstaben benannt. Daher darf man eigentlich nicht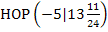 
oder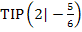 
schreiben. Korrekt ist dagegen die Benennung 
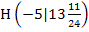für den Hochpunkt bzw. 
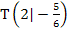für den Tiefpunkt, so wie es auch oben schon geschrieben wurde. Leider beginnt auch das Wort „Terrassenpunkt“ mit T, so dass auch Terrassenpunkte mit T bezeichnet werden müssten. Daher schreibt man bei Funktionen, die sowohl einen Tiefpunkt als auch einen Terrassenpunkt besitzen, dann doch TIP und TEP als Benennung dieser Punkte;man kann ja nicht zwei verschiedene Punkte zugleich mit T bezeichnen. Manchen Lehrern ist die korrekte Bezeichnung eines Punktes mit einem Großbuchstaben auch gar nicht so wichtig, anderen dagegen schon. Achte einfach genau darauf, wie Dein(e) Lehrer(in) die Punkte benennt. Genauso machst du es dann auch.
Dein(e) Lehrer(in) in der Schule setzt nicht irgendwelche Zahlen aus den jeweiligen Bereichen der Monotonietabelle in die Ableitung ein, um die entsprechenden Vorzeichen der mittleren Zeile zu ermitteln, sondern er/sie verwendet dazu eine Skizze des Graphen der Ableitungsfunktion? Dann solltest du das ebenfalls so machen. Allerdings funktioniert das nur bei relativ einfachen Funktionen. Mehr dazu bei:Vorzeichen von f´(x) für das Monotonieverhalten graphisch ermitteln
9. Bsp.:
Berechne den Schnittwinkel der Funktion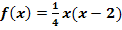 
mit der x-Achse in ihrer positiven Nullstelle! Runde dabei auf 2 Dezimalen!
Lösung:
Unter dem Schnittwinkel einer Funktion mit der x-Achse versteht man den Winkel zwischen der entsprechenden Tangente des Funktionsgraphen und der x-Achse. In diesem Aufgabenbeispiel ist nach dem Schnittwinkel von 
in ihrer positiven Nullstelle gefragt. Deshalb berechnen wir vorweg alle Nullstellen der Funktion. Später werden wir natürlich nur mit der positiven Nullstelle weiterrechnen.
Nst.: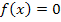 
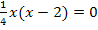
An dieser Stelle solltest du auf keinen Fall die Klammer mit der zweiten binomischen Formel auflösen und ausmultiplizieren. Dies würde das Ganze nämlich nur komplizierter machen! Erinnere dich an den folgenden Satz:Ein Produkt ist gleich Null, wenn einer der Faktoren gleich Null ist. Daher können wir unsere Gleichung ganz bequem lösen, indem wir jeden Faktor, also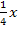 
und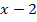 
, einzeln gleich Null setzen.
