b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

Nach diesem Schritt sieht die Tabelle folgendermaßen aus:

x		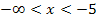		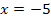	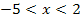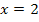2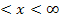
	+	0		0

Jetzt bleibt noch der letzte Bereich 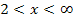  . Du solltest jetzt selbständig in der Lage sein, das Vorzeichen von in diesem Bereich zu ermitteln.

Du kannst dazu zum Beispiel die Zahl 3 in einsetzen.

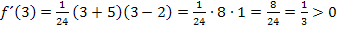
Es ergibt sich für ein positives Ergebnis;wir tragen daher ein Pluszeichen unterhalb von 2 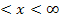in die Tabelle ein.

Nun sieht die Tabelle so aus:

x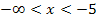
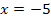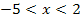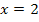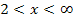	+	0		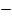0	+

Jetzt müssen wir in die unterste Zeile der Tabelle eintragen, ob der Graph in den jeweiligen Bereichen steigt bzw. fällt. Das hängt natürlich von den Vorzeichen der Ableitung ab. Ist die Ableitung positiv (+), dann steigt streng monoton. Ist die Ableitung negativ (-), dann fällt streng monoton. Dies tragen wir jeweils in der untersten Zeile ein. Mit Pfeilen lässt sich dies ebenfalls schön darstellen.

x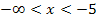
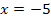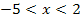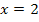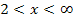	+	0		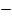0	+
	streng monoton steigend		streng monoton fallend		streng monoton steigend

Zum Schluss müssen wir uns noch überlegen, ob an den Stellen x = -5 und x = 2 jeweils ein relativer Hochpunkt (HOP), ein relativer Tiefpunkt (TIP) oder ein Terrassenpunkt(TEP) vorliegt. Das erkennt man eigentlich sehr gut am Verlauf der Pfeile.

Betrachten wir als erstes die Stelle x = -5. Links davon, also für 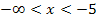, steigt der Graph. Rechts davon, also für 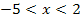, fällt der Graph. Es muss bei x = -5 demnach ein relativer Hochpunkt (HOP) vorliegen. An Hand der Pfeile 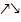(Vergleiche Tabelle!) kannst du dies bestimmt nachvollziehen.

Als letztes betrachten wir nun die Stelle x = 2. Links davon, also für 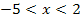, fällt der Graph. Rechts davon, also für 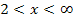, steigt der Graph. Es muss demnach bei x = 2 ein relativer Tiefpunkt (TIP) vorliegen. Mit den Pfeilen 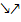(Vergleiche Tabelle!) sollte dir dies einleuchten.

Einen Terrassenpunkt (TEP) gibt es hier überhaupt nicht, da sich bei einem Terrassenpunkt das Vorzeichen von nicht ändert. In der Monotonietabelle müsste bei einem Terrassenpunkt also entweder  +  0 +  oder  –  0  –  stehen. Das kommt in unserer Tabelle aber nicht vor;sowohl bei x = -5 als auch bei x = 2 liegt ein Vorzeichenwechsel von vor.

Die fertige Monotonietabelle sieht dann folgendermaßen aus:

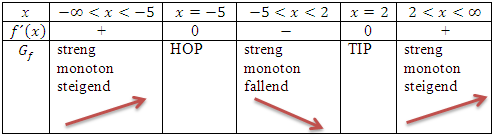
Alternativ kann in der Monotonietabelle auch die Intervallschreibweise verwendet werden:

Speziell für Schüler einer FOS in Bayern:In manchen Aufgaben wird nach den sogenannten „Monotonie-Intervallen“ gefragt. Das kann auch folgendermaßen formuliert sein:„Geben sie die größtmöglichen Bereiche an, wo die Funktion streng monoton steigend bzw. fallend ist.“ Dann reicht die Monotonietabelle nicht! Du musst bei dieser Aufgabenstellung zusätzlich zur Tabelle gesondert alle Intervalle aufschreiben, in denen die Funktion streng monoton steigt bzw. fällt. Dabei müssen alle Schüler einer FOS die Ränder der einzelnen Intervalle jeweils miteinschließen! (Dies gilt aber nicht für Gymnasiasten! Auf dem Gymnasium schreibt man die Ränder grundsätzlich ausgeschlossen.) D.h. alle Schüler einer FOS müssen die eckigen Klammern in der Intervallschreibweise zu den Zahlen hin gerichtet schreiben bzw. das Kleiner-Gleich-Zeichen an Stelle des Kleiner-Zeichens bei der Angabe der Intervalle verwenden, außer bei 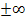. Daher musst du natürlich auch 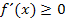bzw. 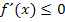schreiben und nicht bloß 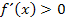bzw. 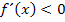.) Mehr dazu speziell für alle Schüler einer FOS:Monotonie-Intervalle angeben

---