b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Ableitung (unfaktorisiert):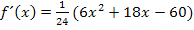 
Von oben wissen wir:
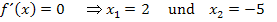
Ableitung (faktorisiert):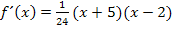 
Als nächstes ermitteln wir jeweils die Vorzeichen von 
in den Bereichen 
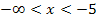, -5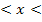 
2 und 2 
.
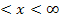Dabei beginnen wir ganz links in der Tabelle, also mit 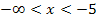. Wir wählen eine beliebige Zahl aus diesem Bereich, beispielsweise -6, und setzen sie in ein.
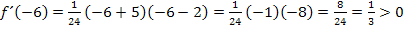
Das Vorzeichen von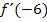 
ist positiv, daher tragen wir unterhalb von 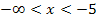ein Pluszeichen in die Tabelle ein.
Eigentlich muss man gar nicht den genauen Wert von 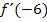berechnen, sondern nur das Vorzeichen. Es reicht daher völlig, sich nur die Vorzeichen der einzelnen Faktoren von für x = -6 zu überlegen:Der Faktor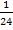 
ist sowieso positiv. Die erste Klammer (x + 5) ergibt etwas Negatives, wenn man für x die Zahl -6 oder eine andere Zahl kleiner -5 einsetzt. Die zweite Klammer (x – 2) ergibt auch etwas Negatives, wenn man für x die Zahl -6 oder eine andere Zahl kleiner -5 einsetzt. Wegen 
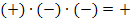ergibt sich insgesamt ein positives Vorzeichen.
Mit der faktorisierten Form von kannst du dir, wie soeben erklärt, ganz schnell die Vorzeichen in den einzelnen Bereichen überlegen. Daher ist die faktorisierte Form von praktischer als die unfaktorisierte. Verwendest du die unfaktorisierte Form von musst du wirklich den genauen Wert ausrechnen, da sich anders das Vorzeichen nicht bestimmen lässt.
Das in die Tabelle neu eingetragene Pluszeichen ist gelb unterlegt, damit du es direkt erkennen kannst. Nach diesem Schritt sieht die Tabelle folgendermaßen aus:
| x | |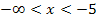
 |
 |
 |
 |
|
 + |
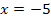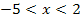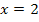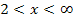0 | 0 | ||
 |
Entsprechend geht es jetzt weiter mit dem Bereich 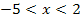. Überlege dir jetzt selbst das Vorzeichen von in diesem Bereich, bevor du weiter liest!
Du hast dir inzwischen hoffentlich irgendeine Zahl zwischen -5 und 2 gedacht, in eingesetzt und das Vorzeichen ermittelt. Du müsstest dann herausgefunden haben, dass für 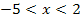ein negatives Ergebnis bei der Ableitung herauskommt. Falls dir das nicht klar ist, hier noch einmal alles ganz ausführlich:Wir denken uns eine Zahl zwischen -5 und 2. Nehmen wir ´mal die Zahl 1. Wir setzen sie in ein. Entweder du rechnest den genauen Wert von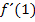 
aus oder du überlegst dir nur die Vorzeichen der einzelnen Faktoren und folgerst daraus das gesamte Vorzeichen in diesem Bereich.
Hier noch einmal die Ableitung (faktorisiert):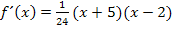
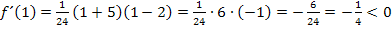
Alternativ dazu:Vorzeichenüberlegung, wenn x eine Zahl zwischen -5 und 2 darstellt, beispielsweise x = 1.
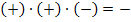
Auf jeden Fall ergibt sich ein negativer Wert für im Bereich 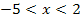. Wir tragen daher ein Minuszeichen (in der nächsten Tabelle gelb unterlegt) in die Monotonietabelle unterhalb vo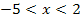n ein.
