b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Vorweg noch einmal zur Erinnerung:
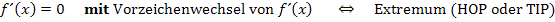
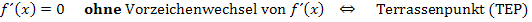
Untersuchung der Art der Extrema mit Hilfe der Monotonie:
Von oben wissen wir:
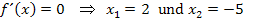
Anleitung zum Erstellen der Monotonietabelle:
Als erstes zeichnest du eine Tabelle mit drei Zeilen. In die oberste Zeile kommen die x-Werte, in die mittlere Zeile werden später die Vorzeichen von 
eingetragen und in die unterste Zeile, ob 
steigt, fällt bzw. einen HOP, TIP oder TEP hat. (Das ist bei jeder Monotonietabelle so.)
Die Anzahl der Spalten hängt jedoch von der Anzahl der Punkte mit waagrechten Tangenten ab;also davon, wie viele Lösungen sich aus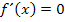 
ergeben haben. (Das muss man natürlich immer schon vorher ausgerechnet haben, bevor man eine Monotonietabelle anfertigen kann.) Es gibt hier zwei Punkte mit waagrechten Tangenten, daher brauchen wir hier sechs Spalten. Warum genau sechs? Betrachte dazu die nächste unten gezeigte Tabelle! In die erste Spalte schreibt man immer von oben nach unten:x, und . Zwei schmale Spalten braucht man für x = -5 und x = 2. (In der Zeile für , kann man unter x = -5 und x = 2 übrigens gleich eine Null eintragen, da hier die Ableitung schließlich gleich Null ist.) Die restlichen drei etwas breiteren Spalten benötigen wir für die Zahlenbereiche, wo x kleiner ist als -5, zwischen -5 und 2 liegt, sowie größer als 2 ist. Achte beim Eintragen der Zahlen x = -5 und x = 2 darauf, dass diese Werte der Größe nach geordnet in die Monotonietabelle geschrieben werden müssen, also zuerst -5, dann rechts davon die Zahl 2. Die oberste Zeile der Tabelle kannst du dir dabei als eine Art Zahlenstrahl vorstellen;dort steht schließlich die Zahl -5 ebenfalls links von der Zahl 2, weil -5 ja kleiner ist wie 2.
Deine Tabelle sollte anfangs aussehen, wie die folgende:
| x |  |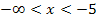
 |
 |
 |
 |
|
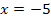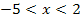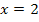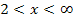0 | 0 | |||
|
Nun müssen wir uns die Vorzeichen von in den jeweiligen Bereichen überlegen. Dazu setzt man beispielsweise irgendeine Zahl in die Ableitung ein, die in dem entsprechenden Bereich liegt.
Vorsicht:Nicht in die Funktionsgleichung 
einsetzen, sondern wirklich in die Ableitung 
! Wir suchen schließlich die Vorzeichen von und nicht von .
Am einfachsten lassen sich die Vorzeichen von im Kopf an der faktorisierten Form der Ableitung feststellen. Daher faktorisieren wir die Ableitung, bevor wir unsere Beispielwerte für x einsetzen. (Wenn du beim Faktorisieren unsicher bist, setzt du besser in die unfaktorisierte Form von ein und verwendest beim Ausrechnen einfach den Taschenrechner. Das funktioniert natürlich auch.) Erklärungen zum Faktorisieren eines Funktionsterms findest du unter Faktorisierter Funktionsterm. Hier musst du natürlich nicht , sondern die Ableitung faktorisieren. aber das geht entsprechend.
