b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
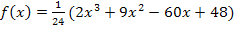
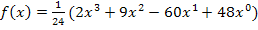
Für die Ableitung ergibt sich:
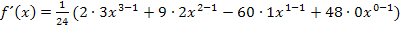
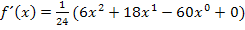
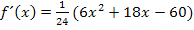
So ausführlich solltest du das selbst allerdings nicht schreiben;die Zwischenschritte wurden hier nur zur Erklärung gezeigt. Du solltest eigentlich direkt von 
, wie es in der obersten Zeile steht, auf 
in der untersten Zeile kommen. Die Zwischenschritte würden dich zu viel Zeit kosten.
Nun setzten wir die Ableitung gleich Null;wir suchen schließlich nach Punkten mit waagrechten Tangenten.
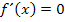
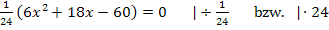
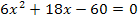
Du kannst diese Gleichung jetzt entweder sofort mit der Mitternachtsformel lösen oder vorher alles noch durch 6 teilen. Wir entscheiden uns hier dazu, vorher noch durch 6 zu dividieren;dadurch werden die Zahlen kleiner und es rechnet sich anschließend leichter.
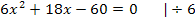
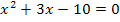
Einsetzen in die Mitternachtsformelergibt nun:
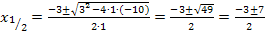
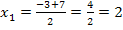
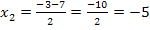
Da sich zwei verschiedene Werte für x ergeben haben, gibt es bei der Funktion auch genau zwei Punkte mit waagrechten Tangenten, nämlich bei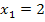 
und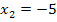 
. Dies sind schon die gesuchten x-Koordinaten dieser beiden Punkte.
Wäre in der Aufgabe ausschließlich nach den Abszissen (x-Koordinaten) der Punkte mit waagrechter Tangente gefragt gewesen, dann wäre man jetzt schon fertig. Hier ist allerdings nach „Art und Lage“, also nicht nur nach den Abszissen, der Extrema gefragt. Weil die Bestimmung der Lage, also die Berechnung der x- und y-Koordinaten, verlangt ist, müssen wir zusätzlich zu den x-Koordinaten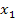 
und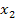 
auch die entsprechenden y-Koordinaten 
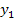und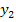 
berechnen. Dazu setzt man 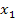und 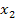jeweils für x in die Funktionsgleichung von ein.
Vorsicht: Niemals in die Ableitung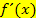 
einsetzen, wenn du die y-Koordinate eines Kurvenpunktes von 
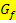berechnen willst, denn 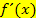ist ja die Steigung von 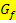und nicht y! Würdest du die x-Koordinaten in die Ableitung einsetzen, würdest du die Steigung an dieser Stelle erhalten und die ist bei Punkten mit waagrechter Tangente immer gleich Null. (Mit dem Ansatz 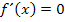haben wir die x-Koordinaten schließlich ermittelt.) Also immer in die Funktionsgleichung 
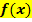einsetzen, wenn du die y-Koordinate eines Kurvenpunktes der Funktion 
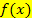ermitteln sollst. Es gilt schließlich: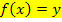 
Völlig egal, wie du x berechnet hast:Um y eines Kurvenpunktes von 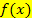zu berechnen, immer x in die Funktionsgleichung 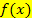einsetzen und nicht in die Ableitung !
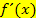Hier noch einmal die Funktionsgleichung: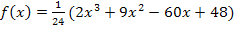
Berechnung der y-Koordinaten der beiden Punkte mit waagrechter Tangente:
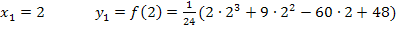
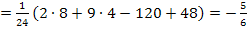
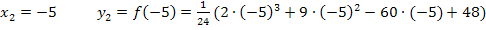
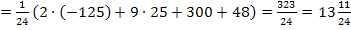
Sorry, dass die y-Koordinaten hier so unmögliche Zahlen ergeben, doch sollst du dich gleich ´mal daran gewöhnen, dass vor allem bei y-Koordinaten schon ´mal so doofe Zahlen herauskommen können. Das Ergebnis muss deshalb noch lange nicht falsch sein! Lass dich daher von unangenehmen y-Koordinaten nicht irritieren. Soll in einer Aufgabe aber auch der Funktionsgraph gezeichnet werden, ist es eher unwahrscheinlich, dass die y-Koordinaten der Extrema extrem großbzw. klein sind. Dann liegt wahrscheinlich doch ein Fehler in deiner Rechnung vor.
