b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Hat der Graph der Ableitungsfunktion bei x = a eine Nullstelle mit Vorzeichenwechsel, dann hat der Graph 
der Funktion 
bei x = a ein relatives (lokales) Extremum. Es kann sich dabei um einen relativen Tiefpunkt oder um einen relativen Hochpunkt handeln, je nach dem, ob zuerst fällt und dann steigt oder umgekehrt. Mit den Begriffen relativer (lokaler) Tiefpunkt/Hochpunkt ist gemeint, dass dieser Punkt in der näheren Umgebung von x = a der tiefste/ höchste Punkt ist;er muss aber nicht der absolut höchste/ tiefste Punkt des ganzen Graphen sein. (Absolut höchste und tiefste Punkte eines Graphen bezeichnet man dagegen als absolute bzw. globale Extrempunkte.)
Von den Extrempunkten sind die sogenannten Terrassenpunkte zu unterscheiden. Auch bei einem Terrassenpunkt hat der Graph der Funktion eine waagrechte Tangente, doch ändert sich an dieser Stelle das Steigungsverhalten (Monotonie/Monotonieverhalten) von nicht.
Hat der Graph 
der Ableitungsfunktion bei x = a eine Nullstelle ohne Vorzeichenwechsel, d.h. berührt die x-Achse nur, schneidet sie aber nicht, dann hat der Graph der Funktion bei x = a einen Terrassenpunkt (TEP). Dies erkennt man auch gut an einer Monotonietabelle.
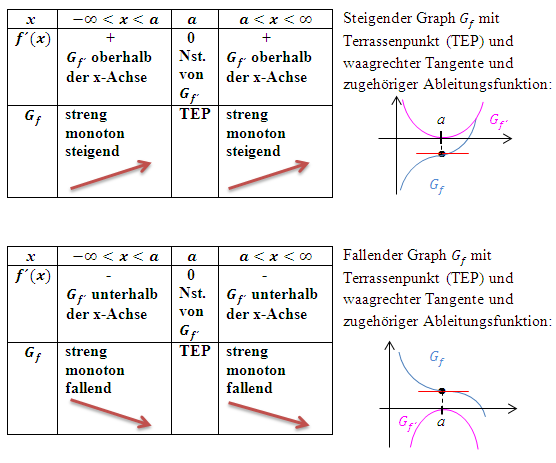
Im Folgenden sind zwei verschiedene Beispiele einer Monotonietabelle mit Terrassenpunkt von an der Stelle x = a dargestellt. (Dabei steht der Buchstabe a für eine konkrete reelle Zahl.) Entsprechend hat der Graph der Ableitungsfunktion bei x = a eine Nullstelle ohne Vorzeichenwechsel.
Als nächstes kannst du im Unterschied zu den Monotonietabellen ohne Vorzeichenwechsel von 
, die wir oben gesehen haben, nun ein Beispiel einer Monotonietabelle mit zweimaligen Vorzeichenwechsel von sehen. Der Graph der Ableitungsfunktion besitzt zwei verschiedene Nullstellen jeweils mit Vorzeichenwechsel, in diesem Beispiel bei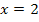 
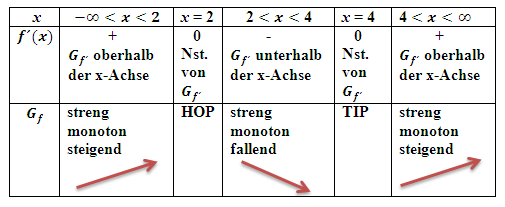
und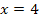 
. (Diese Zahlen sind nur ein beliebiges Beispiel.) Entsprechend hat der Graph einen relativen Hochpunkt (HOP) und einen relativen Tiefpunkt (TIP):
Einige Lehrer(innen) schreiben an Stelle von am Anfang der zweiten Zeile der Monotonietabelle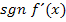 
und statt dem Pluszeichen in der Tabelle die Zahl 
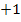bzw. statt dem Minuszeichen die Zahl 
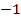. Das sieht dann folgendermaßen aus:
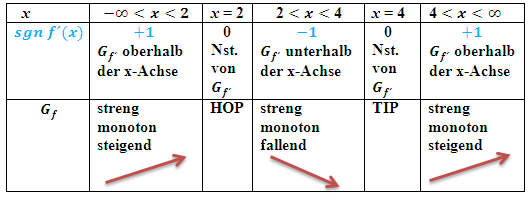
Streng mathematisch ist dies die korrekte Schreibweise, doch ist das nicht so schülerfreundlich. Daher werden auf dieser website alle folgenden Monotonietabellen in der zuerst gezeigten (nicht hundertprozentig mathematisch korrekten) Form ohne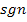 
geschrieben. Die meisten Lehrer(innen) machen das auch so. Die Abkürzung 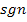steht für „signum“ (lat. signum = Zeichen, Vorzeichen). Mit 
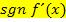ist das Vorzeichen der Ableitung gemeint und nur das Vorzeichen von schreiben wir ja immer in die einzelnen Spalten der zweiten Zeile der Monotonietabelle. Warum bei der Schreibweise mit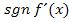 
statt + die Zahl 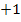geschrieben wird und statt – die Zahl 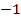, wird erst verständlich, wenn man weiß, wie die Signum-Funktion 
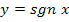definiert ist. Sie ordnet jeder positiven Zahl die Zahl 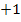zu, jeder negativen Zahl die Zahl 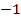und der Null wieder die Null. (Mehr zur Signum-Funktion im Kapitel:Betragsfunktion, Signum-Funktion und Gaußsche Treppenfunktion) Sollte dein(e) Lehrer(in) in der Schule allerdings die Schreibweise 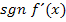verwenden, musst du das ebenfalls machen, ansonsten bekommst du in Prüfungen Punkte abgezogen. Statt Plus + musst du dann auch 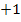und statt Minus – die Zahl 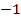in der mittleren Spalte der Monotonietabelle schreiben.
