b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
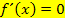
Manche Lehrer(innen) würden an dieser Stelle über dem Gleichheitszeichen ein kleines Ausrufezeichen schreiben: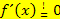 
Das ist streng mathematisch gesehen auch notwendig. Das Gleichheitszeichen mit dem Ausrufezeichen darüber bedeutet so viel wie „soll gleich sein“ oder „es soll gelten, dass…“. Du schreibst es am besten genauso, wie dein(e) Lehrer(in) in der Schule. Setzt er/sie beim Ansatz das Ausrufezeichen über das Gleichheitszeichen, dann machst du es ebenfalls;schreibt er/sie ein normales Gleichheitszeichen, kannst du das auch so machen.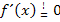 
bedeutet also, dass die Ableitung gleich Null sein soll. Wir bleiben aber auf dieser website bei der einfacheren Schreibweise 
.)
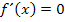Hinweis:Weil die Bedingung 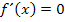bei einem Extremum gelten muss, also notwendig ist, bezeichnet man dies auch als „notwendige“ Bedingung für einen relativen Extrempunkt. Damit überhaupt ein relatives Extremum vorliegen kann, ist es notwendig, dass 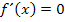gilt. Damit ist es aber noch nicht sicher, dass wirklich ein relatives Extremum (HOP oder TIP) vorliegt, denn es könnte sich ja auch um einen Terrassenpunkt handeln und Terrassenpunkte sind bekanntlich keine Extrempunkte!
Für den Nachweis, dass tatsächlich ein relatives Extremum vorliegt, benötigen wir zusätzlich zur notwendigen Bedingung 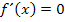, noch eine „hinreichende“ Bedingung. D.h. eine Bedingung, die sicherstellt, dass es sich wirklich hundertprozentig um ein Extremum und nicht etwa um einen Terrassenpunkt handelt. Als hinreichende Bedingung kann entweder der Vorzeichenwechsel der ersten Ableitung oder 
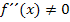verwendet werden. Sollte dir die zweite Ableitung 
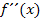momentan noch nicht bekannt sein, ist das nicht schlimm. Wir werden hier die Extrema an Hand ihres Vorzeichenwechsels der ersten Ableitung nachweisen. (Für Schüler, die die zweite Ableitung 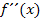schon kennen und gerne auch diesen Lösungsweg sehen wollen, kommt an der entsprechenden Stelle ein link dazu.)
Nun leiten wir die Funktion 
einmal ab und setzen danach die Ableitung gleich Null.
Zum Ableiten verwenden wir die Ableitungsregel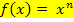 
mit n 
ℝ 
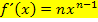. Der Faktor 
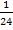muss nicht in die Klammer hinein multipliziert werden;man kann ihn beim Ableiten einfach vor der Klammer stehen lassen. (Zur Erinnerung:Multiplikative Konstanten bleiben beim Ableiten stehen, wogegen Konstanten, die addiert oder subtrahiert werden, wegfallen. Dass Zahlen ohne x, die in 
addiert oder subtrahiert werden, beim Ableiten wegfallen, kann man sich auch mit einem hinzugefügten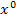 
erklären. Es gilt ja 
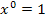. Das kannst du dir gleich im Folgenden anschauen.)
