b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

So kommt man auf das richtige Ergebnis:

Nun können wir die berechnete Ableitung gleich setzen.

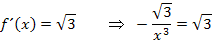
Löse nun die Gleichung selbständig nach x auf!

Du weißt nicht, wie man das macht? Ok, das geht folgendermaßen:Zuerst mit dem Nenner multiplizieren. Dadurch kommt auf die rechte Seite der Gleichung und steht vor allem nicht mehr im Nenner. Dann durch dividieren, damit alleine steht. Nun muss x noch vom Exponenten „befreit“ werden. Um „hoch 3“ weg zu bekommen, muss die dritte Wurzel gezogen werden. Jetzt solltest du es wirklich selbst rechnen können.

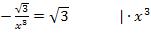
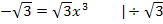
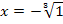
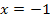
Noch ein kleiner Hinweis:Das Minus-Zeichen bei 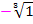darf keinesfalls unter der Wurzel stehen!

Nun kennen wir die x-Koordinate des Punktes P, in dem die Tangente mit dem Neigungswinkel 60° den Funktionsgraphen berührt. Die y-Koordinate von P müssen wir noch berechnen, da wir sie nachher zur Berechnung des y-Achsenabschnitts t der Tangente brauchen. Es ist schließlich die gesamte Tangentengleichung im Punkt P gesucht und nicht nur die Steigung. Die y-Koordinate von 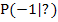wird berechnet, indem die x-Koordinate 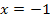in die Funktionsgleichung 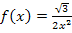eingesetzt wird.

Die Tangentensteigung kennen wir bereits, da wir sie oben schon ermittelt haben. Es gilt:

Es fehlt von der Tangentengleichung nur noch der y-Achsenabschnitt t. Wir erhalten ihn, indem wir m und die Koordinaten von 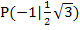für x und y in die allgemeine Geradengleichung einsetzen und nach t auflösen.

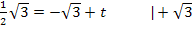
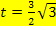
Nun müssen nur noch die berechneten Werte für m und t in die allgemeine Geradengleichung eingesetzt werden. Dann ist die gesuchte Tangentengleichung ermittelt.

Sie lautet: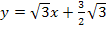

Fertig!

Es soll an dieser Stelle noch einmal auf die entscheidenden Schritte bei dieser Aufgabe hingewiesen werden:

Da der Schnittwinkel 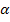der Tangente mit der x-Achse angegeben war, ließsich die Tangentensteigung m berechnen mit der Formel:

Dann wurde der für m berechnete Wert mit der Ableitung 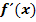gleichgesetzt, da die Ableitung schließlich der Tangentensteigung m entspricht.

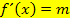
Dadurch entstand eine Gleichung, die man nach x auflösen konnte. So ergab sich die x-Koordinate des Berührpunktes P.

Dieses Prinzip musst du dir unbedingt merken! Hat man die x-Koordinate des Kurvenpunktes erst einmal berechnet, lässt sich im Anschluss die Tangentengleichung leicht aufstellen.

8. Bsp.:

Gegeben ist die Funktion . Berechne die Art und Lage ihrer Extrema!

Lösung:

Es sollen Art und Lage der Extremader Funktion ermittelt werden. Mit der Lage eines Extremums sind einfach seine x- und y-Koordinaten gemeint. Unter der Art eines Extremums versteht man, die Unterscheidung zwischen Hochpunkt und Tiefpunkt. In jedem Extrempunkt von 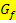verläuft die Tangente an 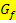waagrecht. Wir müssen also zuerst die x-Koordinaten aller Punkte mit waagrechter Tangente berechnen. (Zu den Punkten mit waagrechter Tangente gehören übrigens auch die Terrassenpunkte, die jedoch nicht zu den Extrema zählen.) Da bei allen Punkten mit waagrechter Tangente die Tangentensteigung, d.h. die Ableitung , zwangsläufig gleich Null sein muss, gilt bei allen Punkten mit waagrechter Tangente:

---