b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

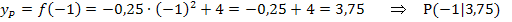
7. Bsp.:

Wie lautet die Gleichung der Tangente an die Funktion , welche die x-Achse unter einem 60°-Winkel schneidet?

Lösung:

Eine Zeichnung im Koordinatensystem ist hier zwar nicht verlangt, doch kannst du dir den Zusammenhang mit einer Skizze bestimmt besser vorstellen. Wir zeichnen zuerst ein Koordinatensystem mit dem Graph der Funktion 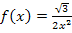. Gesucht ist die Tangente an den Graph, welche die x-Achse unter einem 60°-Winkel schneidet. Daher nimmst du dein Geodreieck, legst es im 60°-Winkel zur x-Achse und verschiebst es so lange, bis es den Funktionsgraphen in genau einem Punkt berührt. So kannst du die gesuchte Tangente einzeichnen.

Hinweis:Den Graph der Funktion 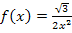kannst du entweder mit einer Wertetabelle exakt zeichnen oder nur eine grobe Skizze von anfertigen, wenn du direkt an der Funktionsgleichung erkennst, wie der Graph ungefähr aussehen muss.

Die Funktion 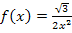ist eine gebrochenrationale Funktion mit der Definitionsmenge . Die Definitionslückeist somit bei x = 0. (Für x kann die Zahl 0 nicht eingesetzt werden, da sonst der Nenner Null ergibt und die Division durch Null nicht definiert ist.) Die y-Achse hat bekanntlich die Gleichung x = 0. Daher ist die y-Achse senkrechte Asymptote der Funktion 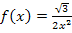. Der Graph ist also eine Hyperbel, welche die y-Achse als senkrechte Asymptote (Pol ohne Vorzeichenwechsel) hat.

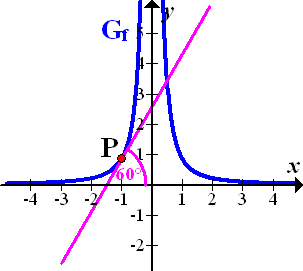
Abb.:Graph der Funktion 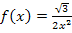mit der gesuchten Tangente, welche die x-Achse unter einem Winkel von 60° schneidet

Nun zum rechnerischen Lösungsweg der Aufgabe. Gesucht ist die Gleichung der Tangente an , welche die x-Achse unter einem Winkel von 60° schneidet. Da eine Tangente eine Gerade ist, hat sie die allgemeine Form . Es müssen also die Tangentensteigung m und der y-Achsenabschnitt t berechnet werden.

Es ist der Schnittwinkel der Tangente von mit der x-Achse gegeben;dieser Winkel ist 60°. Von diesem Winkel kommt man zur gesuchten Tangentensteigung m mit der Formel, die wir im Bsp. 5a.) schon kennengelernt haben:

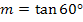
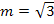
Die Tangentensteigung m ist somit , sie entspricht auch der Ableitung . Daher gilt im Berührpunkt P:

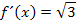
Jetzt müssen wir natürlich erst noch bilden, bevor wir die Ableitung mit gleichsetzen und nach x auflösen können. Versuche nun die Funktion 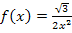selbständig abzuleiten, ohne vorher auf die nachfolgende Lösung zu schauen!

Hast du alleine versucht die Ableitung zu berechnen? Dann müsstest du letztendlich auf folgendes Ergebnis gekommen sein:

Wenn du nicht zu diesem Ergebnis gekommen bist, hier ein paar kleine Tipps:Forme die Funktion zuerst mit Hilfe des Potenzgesetzes um. Dann kannst du die Ableitungsregel verwenden.

---