b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

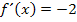
Daher bilden wir schnell die Ableitung und setzen sie dann mit der Steigung der Geraden -2 gleich.

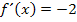
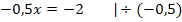
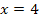
Dies ist schon die x-Koordinate des gesuchten Berührpunktes P. Jetzt fehlt nur noch die y-Koordinate von P. Um sie zu berechnen, muss die soeben berechnete x-Koordinate in die Funktionsgleichung von 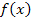eingesetzt werden.

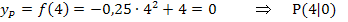
zu 6b.)

Geg.: 

Gesucht sind die Koordinaten des Punktes auf dem Funktionsgraphen , wo die Tangente senkrecht zur Gerade g verläuft. Wenn du dir nicht genau vorstellen kannst, was hier eigentlich berechnet werden soll, fertigst du erst ´mal wieder eine Skizze an. Du kannst natürlich von deiner Zeichnung in 6a.) ausgehen und einfach die neue Gerade dazu zeichnen. Die Tangente an soll nun nicht mehr parallel, sondern senkrecht zur Gerade g verlaufen. Um diese Tangente zu zeichnen, legst du dein Geodreieck im rechten Winkel zur Gerade g und verschiebst es so lange, bis es die Parabel in genau einem Punkt berührt. Diesen Berührpunkt suchen wir. Deine Zeichnung sollte im Prinzip aussehen wie die folgende Abbildung.

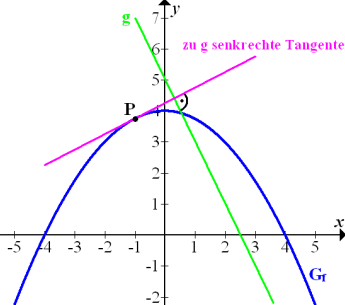
Abb.:Graph der Funktion 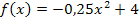und der Gerade 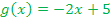mit zu g senkrechter Tangente an .

Aus der Mittelstufe weißt du vermutlich noch:Zwei Geraden stehen aufeinander senkrecht, wenn ihre Steigungen multipliziert -1 ergeben. (Näheres dazu bei:Zueinander senkrechte (orthogonale) Geraden)

Die Gerade g und die Tangente an sollen laut Angabe aufeinander senkrecht stehen. Daher gilt der folgende Zusammenhang zwischen der Steigung der Geraden g und der Tangentensteigung :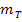

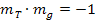
Wir kennen die Gleichung und somit auch die Steigung der Geraden g. Es gilt: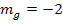 

Somit können wir die Steigung der zu g senkrechten Tangente von leicht ausrechnen, indem wir die Formel nach 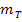auflösen und die Steigung der Geraden 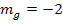einsetzen.

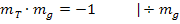
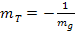
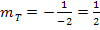
TIPP:  Du brauchst nur bei der bekannten Steigung 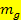das Vorzeichen umdrehen und den Kehrwert bilden, um die Steigung 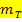der gesuchten zu g senkrechten Geraden zu finden. In diesem Beispiel wird aus 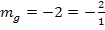die Steigung 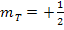der senkrechten Geraden. Also einfach das Vorzeichen der Steigung umdrehen, sowie Nenner und Zähler gegen einander vertauschen, um die Steigung 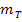der zu g senkrechten Geraden zu finden.

Die Tangente an die Parabel muss daher die Steigung 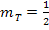haben. Die Tangentensteigung der Funktion 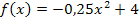entspricht bekanntlich ihrer Ableitung . Somit gilt im Berührpunkt P:

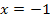
Dies ist schon die x-Koordinate des gesuchten Punktes P. Jetzt fehlt nur noch seine y-Koordinate;wir erhalten sie durch Einsetzen der x-Koordinate 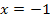in die Funktionsgleichung .

---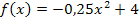