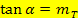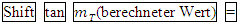b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
3. Wie berechnet man den Schnittwinkel einer Tangente mit der x-Achse?
Geg.: Funktionsgleichung 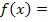 … und Kurvenpunkt … und Kurvenpunkt 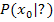
Ges.: Schnittwinkel Anleitung: · · Tangentensteigung d.h. x-Koordinate von P in · Schnittwinkel Den berechneten Wert für Tastenfolge am Taschenrechner (Mode:DEG): |
6.Bsp.:
Gegeben ist die Funktion 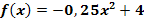 .
.
a.) In welchem Kurvenpunkt verläuft die Tangente an den Graph 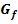 parallel zu der Geraden
parallel zu der Geraden 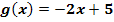 ?
?
b.) In welchem Kurvenpunkt verläuft die Tangente an den Graph 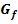 senkrecht zu der Geraden
senkrecht zu der Geraden 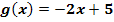 ?
?
Lösung:
Zu 6a.)
Falls du dir im Moment gar nicht vorstellen kannst, was du hier überhaupt ausrechnen sollst, bist du nicht alleine;das geht bei dieser Art von Aufgaben einigen Schülern so. Um dir mehr Klarheit zu verschaffen, solltest du dir erst einmal eine Zeichnung machen, die den Graph der Funktion 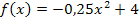 und die Gerade
und die Gerade 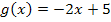 enthält.
enthält.
Brauchst du Hilfe bei der Zeichnung? Hier noch ein paar Tipps:
Die Funktion 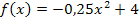 ist eine nach unten geöffnete breitere Parabel mit dem Scheitel S(0|4). Um die Parabel genau zu zeichnen, berechnest du einfach ein paar Funktionswerte im Bereich [-5;5].
ist eine nach unten geöffnete breitere Parabel mit dem Scheitel S(0|4). Um die Parabel genau zu zeichnen, berechnest du einfach ein paar Funktionswerte im Bereich [-5;5].
Die Gerade 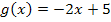 schneidet die y-Achse bei 5. Von dort gehst du 1 nach rechts und 2 nach unten, um das Steigungsdreieck zu zeichnen. Genaueres bei:Lineare Funktionen zeichnen
schneidet die y-Achse bei 5. Von dort gehst du 1 nach rechts und 2 nach unten, um das Steigungsdreieck zu zeichnen. Genaueres bei:Lineare Funktionen zeichnen
Hast du nun die Zeichnung der Parabel und der Gerade angefertigt? Gut, dann verschiebst du die Gerade in Gedanken so weit parallel, bis sie die Parabel berührt, und zeichnest dort eine zweite Gerade. Wo die zweite Gerade die Parabel berührt, liegt der gesuchte Punkt. Es ist schließlich gefragt, in welchem Kurvenpunkt die Tangente an  parallel zur Gerade g verläuft. Du sollst also eine zur Gerade g parallele Gerade zeichnen, die die Parabel in genau einem Punkt berührt. Die Koordinaten dieses Berührpunktes sind hier zu berechnen. Deine Zeichnung sollte nun im Prinzip aussehen wie die folgende Abbildung.
parallel zur Gerade g verläuft. Du sollst also eine zur Gerade g parallele Gerade zeichnen, die die Parabel in genau einem Punkt berührt. Die Koordinaten dieses Berührpunktes sind hier zu berechnen. Deine Zeichnung sollte nun im Prinzip aussehen wie die folgende Abbildung.
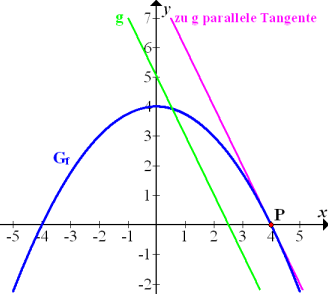
Abb.:Graph  der Funktion
der Funktion 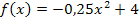 und der Gerade
und der Gerade 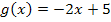 (in Grün) mit zu g paralleler Tangente an
(in Grün) mit zu g paralleler Tangente an  (in Rosa).
(in Rosa).
Wie du weißt, sind zwei Geraden parallel, wenn sie die gleiche Steigung haben. Die Tangente an die Parabel soll parallel zur Gerade 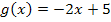 verlaufen. Daher muss die Tangentensteigung gleich der Steigung der Geraden g sein. Da die Gerade g in diesem Beispiel die Steigung m = -2 hat, muss auch die Tangentensteigung gleich -2 sein. Die Tangentensteigung entspricht der Ableitung
verlaufen. Daher muss die Tangentensteigung gleich der Steigung der Geraden g sein. Da die Gerade g in diesem Beispiel die Steigung m = -2 hat, muss auch die Tangentensteigung gleich -2 sein. Die Tangentensteigung entspricht der Ableitung  der Funktion
der Funktion 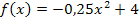 . Daher muss im Berührpunkt P gelten:
. Daher muss im Berührpunkt P gelten:

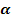 zwischen der Tangente an
zwischen der Tangente an  ableiten
ableiten 
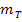 berechnen:
berechnen: 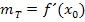
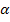 berechnen:
berechnen: