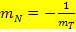b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Entsprechend verfährst du nun mit der Normale 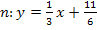 . Der y-Achsenabschnitt ist hier leider eine ziemlich „doofe“ Zahl. Zum Zeichnen kannst du
. Der y-Achsenabschnitt ist hier leider eine ziemlich „doofe“ Zahl. Zum Zeichnen kannst du  verwenden. Zeichne die Normale auch wieder mit Hilfe des y-Achsenabschnitts und des Steigungsdreiecks in dasselbe Koordinatensystem ein. Also, ungefähr 1,8 nach oben auf der y-Achse, von dort 3 nach rechts und 1 nach oben, wegen
verwenden. Zeichne die Normale auch wieder mit Hilfe des y-Achsenabschnitts und des Steigungsdreiecks in dasselbe Koordinatensystem ein. Also, ungefähr 1,8 nach oben auf der y-Achse, von dort 3 nach rechts und 1 nach oben, wegen 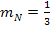 . (Nenner der Steigung immer nach rechts und den Zähler hier nach oben, weil die Steigung positiv ist.) Nun sollte sich eine Gerade ergeben haben, welche die Tangente im Punkt
. (Nenner der Steigung immer nach rechts und den Zähler hier nach oben, weil die Steigung positiv ist.) Nun sollte sich eine Gerade ergeben haben, welche die Tangente im Punkt 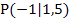 senkrecht schneidet.
senkrecht schneidet.
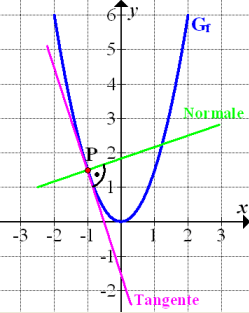
Abb.:Graph der Funktion 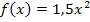 mit Tangente und Normale im Punkt
mit Tangente und Normale im Punkt 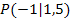
Man hätte die Normale auch ohne ihren y-Achsenabschnitt und ohne Steigungsdreieck ganz leicht zeichnen können. Auf welche Art und Weise lässt sich hier die Normale denn noch viel einfacher einzeichnen? Überlege erst einmal selbst, bevor du weiter liest.
Hast du eine Idee? Denke dabei daran, wie eine Normale definiert ist und, dass die Tangente in P schon eingezeichnet ist!
Eine Normale im Punkt P ist laut Definition eine Gerade, die genau im Punkt P auf der Tangente senkrecht steht. Daher braucht man eigentlich nur im Berührpunkt P der Tangente mit dem Funktionsgraphen eine senkrechte Gerade zur Tangente zeichnen und schon hat man die Normale. Die Normale ist ja eine Lotgerade zur Tangente, welche die Tangente genau in P schneidet. Insofern braucht man die Normalengleichung gar nicht, um die Normale zu zeichnen.
Fassen wir noch einmal alles Wichtige aus diesem Beispiel übersichtlich zusammen. Wir haben folgende Fragestellungen geklärt:
1. Wie ermittelt man eine Tangentengleichung an  im Punkt P?
im Punkt P?
Geg.: Funktionsgleichung 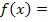 … und Kurvenpunkt … und Kurvenpunkt 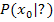
Ges.: Tangentengleichung an Anleitung: · Allgemeiner Ansatz: · y-Koordinate von P berechnen: d.h. x-Koordinate von P in · · Tangentensteigung d.h. x-Koordinate von P in · y-Achsenabschnitt t berechnen: Koordinaten von P für x bzw. y sowie · Tangentengleichung aufstellen: Die berechneten Werte für |
2. Wie stellt man eine Normalengleichung zu  im Punkt P auf?
im Punkt P auf?
Geg.: Funktionsgleichung 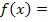 … und Kurvenpunkt … und Kurvenpunkt 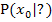
Ges.: Normalengleichung im Punkt P Anleitung: · Allgemeiner Ansatz: · y-Koordinate von P berechnen: d.h. x-Koordinate von P in · · Tangentensteigung d.h. x-Koordinate von P in · Normalensteigung d.h. Vorzeichen von · y-Achsenabschnitt t berechnen: Koordinaten von P für x bzw. y sowie · Normalengleichung aufstellen: Die berechneten Werte für |

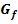 im Punkt P
im Punkt P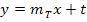
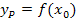
 einsetzen
einsetzen

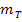 berechnen:
berechnen: 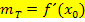
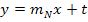
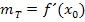
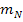 berechnen:
berechnen: