b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Daher bedeutet die Formel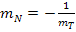 
nichts anderes als, dass man bei der Tangentensteigung 
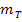das Vorzeichen umdrehen und den Kehrwert bilden muss, um auf die Normalensteigung 
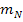zu kommen.
Wieder zurück zu unserer Aufgabe:Wir kennen nun die Normalensteigung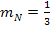 
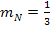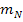. Es fehlt aber noch der y-Achsenabschnitt der Normale;den müssen wir noch berechnen. Dazu setzen wir die ermittelte Steigung für sowie die Koordinaten von 
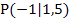für x bzw. y in die allgemeine Geradengleichung ein. Dadurch ergibt sich eine Gleichung, die nur noch die Unbekannte t enthält. Wir müssen dann nur noch nach t auflösen und schon haben wir auch den y-Achsenabschnitt t der Normalen.
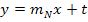
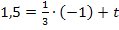
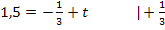
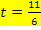
Die Gleichung der Normalen ergibt sich, wenn man 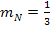und 
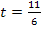in 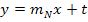einsetzt. Für x und y wird natürlich nichts eingesetzt;sonst würde sich schließlich keine Geradengleichung ergeben;in einer Geradengleichung muss schließlich noch x und y vorkommen! Also jetzt nicht mehr die Koordinaten des Punktes P einsetzen, sondern nur noch 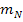und t.
Die Normalengleichung lautet: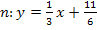 
Damit ist die Aufgabe eigentlich gelöst. Doch solltest du dir zusätzlich eine Zeichnung mit dem Graph der Funktion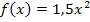 
, der Tangente in 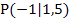und der zugehörigen Normale anfertigen. In der Aufgabenstellung ist zwar keine Zeichnung im Koordinatensystem verlangt, doch solltest du trotzdem für dich selbst auf jeden Fall eine entsprechende Zeichnung anfertigen. Die Zeichnung dient dir einerseits zur Kontrolle der berechneten Tangenten- bzw. Normalengleichung und außerdem zum Überblick. Erst an Hand der Zeichnung siehst du dann, was du überhaupt ausgerechnet hast. Also Papier, Bleistift und Geodreieck zur Hand! Auf geht´s!
Wenn du nicht weißt, wie du das alles schnell zeichnen kannst, hier eine kleine Hilfe:
Die Funktion 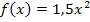kannst du mit Hilfe einiger berechneter Funktionswerte leicht zeichnen;es handelt sich um eine nach oben geöffnete Parabel mit Scheitel S(0|0), die etwas breiter als die Normalparabel ist. (Genaueres bei:Parabeln zeichnen)
Die Tangente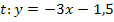 
kannst du folgendermaßen zeichnen:Vom Ursprung (Nullpunkt) des Koordinatensystems gehst du wegen t = -1,5 um 1,5 nach unten;dort schneidet die Tangente die y-Achse. Das ist also dein erster Punkt der Tangente. Den zweiten Punkt bekommst du mit Hilfe des Steigungsdreiecks. Vom Schnittpunkt mit der y-Achse gehst du 1 nach rechts und 3 nach unten, da die Tangentensteigung 
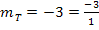ist. Man denkt sich die Steigung einfach als Bruch. Den Nenner geht man dann immer nach rechts und den Zähler in diesem Fall nach unten, weil die Steigung negativ ist. (Bei positiver Steigung wäre man nach oben gegangen. Genaueres bei:Lineare Funktionen zeichnen) Nun hast du zwei Punkte der Tangente;durch diese beiden Punkte zeichnest du jetzt eine Gerade. Somit hast du die Tangente gezeichnet. Wenn du alles richtig gemacht hast, muss die gezeichnete Gerade die Parabel genau im Punkt 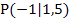berühren.
