b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
zu 5b.)
Geg.: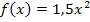 
Gesucht ist die Normalengleichung im Kurvenpunkt 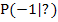. Eine Normale ist eine Gerade, die zur Tangente im Punkt P senkrecht steht und hat somit wie die Tangente eine Gleichung der Form y = mx + t. Um zwischen Tangentensteigung und Normalensteigung unterscheiden zu können, werden hier die Bezeichnungen 
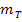für die Tangentensteigung und 
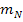für die Normalensteigung verwendet. Die Steigung 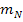und der y-Achsenabschnitt t müssen somit berechnet werden. (Vorsicht:Der y-Achsenabschnitt der Normale ist nicht identisch mit dem y-Achsenabschnitt der Tangente aus Teilaufgabe 5a. Neben der Normalensteigung muss also auch t neu berechnet werden.)
Wir haben bereits in Teilaufgabe 5a.) die y-Koordinate von P berechnet. Wir wissen daher schon, dass gilt:
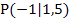
Die Normale steht senkrecht auf der Tangente. In der Mittelstufe hast du irgendwann gelernt:Zwei Geraden mit den Steigungen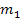 
und 
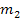sind genau dann zueinander senkrecht, wenn gilt: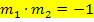 
Siehe auch:Zueinander senkrechte (orthogonale) Geraden
Daher gilt für die Normalensteigung 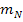und die Tangentensteigung 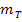die folgende Gleichung: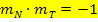 
Die Formel lässt sich leicht nach 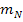auflösen, indem man durch 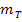dividiert. so ergibt sich für die Normalensteigung:
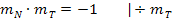
Die Steigung der Tangente in einem bestimmten Kurvenpunkt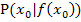 
lässt sich bekanntlich schnell ausrechnen, indem man die x-Koordinate 
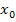des Punktes P in die Ableitung 
einsetzt. D.h. es gilt für die Tangentensteigung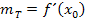 
. Den Ausdruck 
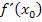setzen wir in die oben gezeigte Formel für 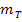ein. Dadurch erhalten wir die folgende Formel für die Normalensteigung, welche sowohl in der orangen bsv-Formelsammlung (für FOS/BOS) als auch auf der Merkhilfe für G8 steht.
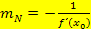
Steigung der Normalen im Punkt 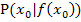, wobei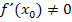 
Hinweis:Mit 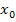ist immer eine konkrete Zahl, nämlich die x-Koordinate des gegebenen Kurvenpunktes P gemeint. In unserem Beispiel ist 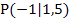und somit 
.
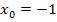In Teilaufgabe 5a.) haben wir die Tangentensteigung in dem Punkt 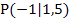schon berechnet. Vergleiche oben! Wir wissen also schon: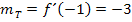 
Für die Normalensteigung in P gilt dann: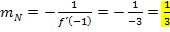 
TIPP: Du kannst die Normalensteigung 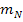auch ganz leicht aus der Tangentensteigung 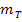bilden, indem du das Vorzeichen von 
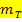umdrehst und außerdem den Kehrwert bildest. Dies folgt nämlich aus der Formel 
.
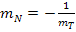Erläuterung zum Tipp:
Das Minus vor dem Bruch bedeutet, dass man das Vorzeichen von 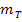umdrehen soll.
Der Bruch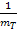 
für sich alleine genommen bedeutet, dass man den Kehrwert von 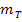bilden soll. Denke dir dabei auch die Tangentensteigung 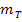als Bruch. 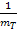heißt dann, dass die Zahl 1 durch den Bruch 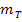geteilt werden soll. Wie du weißt, dividiert man durch einen Bruch, indem man mit dem Kehrwert multipliziert. Deshalb muss man bei 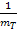die Zahl 1 mit dem Kehrwert von 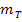multiplizieren. Die Multiplikation des Kehrwerts von 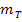mit der Zahl 1 ergibt logischerweise genau den Kehrwert von .
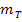