b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

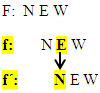
Ebenso gilt umgekehrt:

An der Stelle, wo f´eine Nullstelle hat, hat die Funktion f ein Extremum (oder einen Terrassenpunkt), also einen Punkt mit waagrechter Tangente.

F:  N E W

f: N E W

f´: N E W

Du kannst also von oben nach unten gehen oder andersherum.

So gilt zum Beispiel auch:

An der Stelle, wo f einen Wendepunkt hat, hat die zugehörige Ableitungsfunktion f´ein Extremum, keinen Terrassenpunkt. (Leider ist die „NEW-NEW-NEW“ Methode dabei nicht ganz eindeutig.)

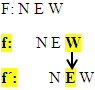
Man kann natürlich auch von f auf F schließen:

An der Stelle, wo f eine Nullstelle hat, hat die zugehörige Stammfunktion F ein Extremum (oder einen Terrassenpunkt).

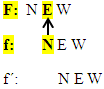
Und wieder andersherum von F auf f schließen:

An der Stelle, wo F ein Extremum (oder einen Terrassenpunkt) hat, hat f eine Nullstelle.

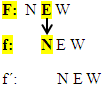
Inzwischen müsste es dir klar sein, wie das „NEW-NEW-NEW“ angewendet wird. Trotzdem noch ein letztes Beispiel.

An der Stelle, wo f ein Extremum hat, hat F einen Wendepunkt oder Flachpunkt.

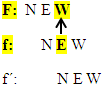
Und andersherum gilt natürlich auch:

An der Stelle, wo F einen Wendepunkt hat, hat f ein Extremum.

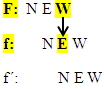
Zwar ist die „NEW-NEW-NEW“ Regel bezüglich der Unterscheidung von Extrema und Terrassenpunkten nicht eindeutig, ebenso nicht bei der Unterscheidung zwischen Wendepunkten und Flachpunkten. Doch trotzdem ist sie oft sehr hilfreich, denn Aufgaben, bei denen es um den Zusammenhang der Graphen von f und f´bzw. F und f geht, sind extrem oft in Klausuren und sogar in der Abi-Prüfung zu finden. Dieser Lehrstoff ist also nicht nur für die nächste Schulaufgabe wichtig, sondern absolute Grundlage für das Mathe-Abi!

Bisher haben wir uns ausführlich mit den Zusammenhängen des Graphen einer bestimmten Funktion und dem Graphen der zugehörigen Ableitungsfunktion befasst. Nun wollen wir uns einige typische Berechnungen mit der Ableitung 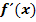ansehen. Solche Aufgaben können dir, zwar in etwas schwieriger Form, aber vom Prinzip her gleich, auch in der Abiturprüfung begegnen.

5. Bsp.:Tangenten- und Normalengleichung aufstellen;Schnittwinkel berechnen

Gegeben ist die Funktion 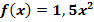und der Kurvenpunkt .

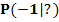a.)  Ermittle die Gleichung der Tangente t im Punkt 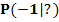. Unter welchem Winkel 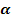schneidet diese Tangente die x-Achse? Runde auf zwei Dezimalen!

b.)  Berechne die Gleichung der Normalen n im Punkt 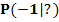. Hinweis:Die Normale im Punkt P ist die Gerade, die im Punkt P zu der Tangente in P senkrecht verläuft.

Lösung:

zu 5a.)

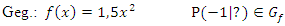
Gesucht ist die Tangentengleichung im Kurvenpunkt 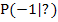. Eine Tangente ist eine Gerade und hat somit eine Gleichung der Form y = mx+ t. Die Steigung mund der y-Achsenabschnitt tmüssen somit berechnet werden.

---