b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Die Zusammenhänge zwischen den Graphen 
und 
machen den meisten Schülern anfangs ziemliche Probleme. Damit das alles etwas klarer wird, schauen wir uns erst einmal ein einfaches Beispiel dafür an.
Funktion:
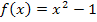
Ableitungsfunktion: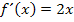 
(Laut Ableitungsregel gilt: 
)
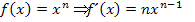Der Graph ist eine nach oben geöffnete Normalparabel mit Scheitel S(0|-1). Die Funktionsgleichung hat ja die Form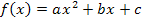 
(mit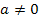 
). Wegen a = 1 handelt es sich, wie gesagt, um eine nach oben geöffnete Normalparabel.
Der Graph der Ableitungsfunktion ist eine Gerade durch den Ursprung mit der Steigung 2. 
hat nämlich die Form 
, wobei m für die Steigung der Geraden und t für ihren y-Achsenabschnitt steht. Da t bei 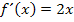fehlt, gilt t = 0 und die Gerade verläuft durch den Ursprung.
In der folgenden Abbildung sind und in einem gemeinsamen Koordinatensystem dargestellt.
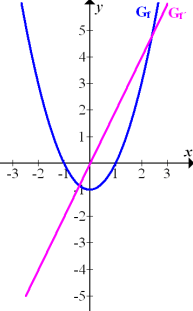
Abb.:Graph der Parabel 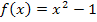und Graph ihrer Ableitung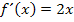
Man kann an dieser Abbildung folgende Zusammenhänge erkennen:
Wo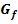 
fällt, liegt 
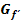unterhalb der x-Achse. Genauer gesagt für 
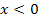(links von der y-Achse) ist streng monoton fallend, daher muss die Tangentensteigung und somit die Ableitung negative Werte annehmen. Die y-Koordinaten der Punkte auf der Ableitungsfunktion haben ein negatives Vorzeichen, was eben für bedeutet, dass er unterhalb der x-Achse verläuft.
Wo 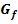steigt, liegt 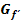oberhalb der x-Achse. Genauer gesagt für 
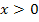(rechts von der y-Achse) ist streng monoton steigend, daher muss die Tangentensteigung und somit die Ableitung positive Werte annehmen. Die y-Koordinaten der Punkte auf der Ableitungsfunktion f´(x) haben ein positives Vorzeichen, was für bedeutet, dass er oberhalb der x-Achse verläuft.
Wo 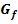eine waagrechte Tangente hat, schneidet 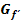die x-Achse. Genauer gesagt für 
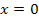(auf der y-Achse) hat seinen Scheitelpunkt, also einen Punkt mit waagrechter Tangente, daher muss die Ableitung gleich Null sein, was für bedeutet, dass er bei 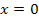eine Nullstelle besitzt. Es handelt sich hier um eine einfache Nullstelle der Ableitung, d.h. schneidet die x-Achse und berührt sie nicht nur. Es liegt hier ein Vorzeichenwechsel bei vor. ( kommt von unterhalb der x-Achse, schneidet die x-Achse und geht dann oberhalb der x-Achse weiter.) Dieser Vorzeichenwechsel der Ableitungsfunktion an der Stelle 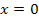ist wichtig, denn daher muss der Graph bei 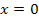ein relatives (lokales) Extremum besitzen. In diesem Fall handelt es sich bei dem Extremum von offensichtlich um einen Tiefpunkt.
Wir halten allgemein fest:
