b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

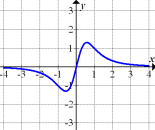
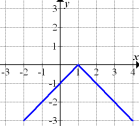
Nun überprüfen wir, ob Abb. 4 umgekehrt die Ableitung von Abb. 6 sein kann. Das ist jedoch auch nicht der Fall, da die in Abb. 6 dargestellte Funktion für 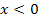und  für 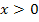streng monoton fallend ist und die zugehörige Ableitungsfunktion unterhalb der x-Achse verlaufen müsste. Der in Abb. 4 gezeigte Graph liegt aber oberhalb der x-Achse. Abb. 4 gehört somit zu keiner der anderen Abbildungen, weder als Funktion noch als Ableitungsfunktion.

Es gibt keine weiteren Paare von Funktion und Ableitungsfunktion bei Abb. 1 bis 6.

Zu 4b.)

Zu den Abbildungen 7 bis 12.

Schau dir die oben gezeigten Graphen von Abb. 7 bis 12 genau an und versuche selbst alle Paare aus Funktion und zugehöriger Ableitung zu finden! Bitte wirklich alleine machen und nicht gleich die folgende Lösung anschauen! Das muss man einfach üben! Also, los geht´s!

Hier noch einmal die sechs Abbildungen:

Abb. 7	Abb. 8	Abb. 9
Abb. 10	Abb. 11	Abb. 12

Hast du es inzwischen wirklich selbstständig probiert, die Lösung zu finden?

Hoffentlich bist du auf folgende Paare gekommen:

Abb. 7 zeigt die Ableitung von Abb. 9

Abb. 10 zeigt die Ableitung von Abb. 12

Abb. 11 zeigt die Ableitung von Abb. 8

Du möchtest genauere Erklärungen, warum das so ist und wie man darauf kommt? Dann gehe zu:Ausführliche Lösung zu Bsp. 4b.)

Wenn du immer wieder bei den Zusammenhängen von und durcheinander kommst, dann solltest du noch einmal die Zusammenfassung am Anfang des Kapitels vor dem 1. Bsp. lesen. Bei Problemen mit den Zusammenhängen von 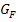und , schaust du dir am besten noch einmal den Kasten am Ende des 2. Beispiels an.

Es gibt dafür aber erfreulicherweise einen wirklich hilfreichen, wenn auch völlig unmathematischen Trick, die „NEW-NEW-NEW“ Methode.

Vielen Schülern, die Schwierigkeiten mit den Zusammenhängen der Graphen von F, f und f´haben, hilft folgender Trick:

Schreibe dreimal das englische Wörtchen „NEW“ (dt. neu) genau um einen Buchstaben versetzt untereinander. Davor kommen die Abkürzungen F (für Stammfunktion), f (für die Funktion selbst) und f´(für die Ableitungsfunktion von f). Das Ganze soll dann folgendermaßen aussehen:

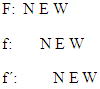
Wie ist das jetzt zu verwenden? Ganz einfach:N steht für Nullstelle, E steht für Extremum (oder eventuell Terrassenpunkt) und W steht für Wendepunkt (oder Flachpunkt).

Konkrete Anwendung der „NEW-NEW-NEW“ Methode:

Zum Zusammenhang von f und f´:

An der Stelle, wo f ein Extremum hat, hat die zugehörige Ableitungsfunktion f´eine Nullstelle.

---