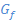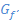b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Nun fragen wir uns, ob der in Abb. 2 gezeigte Graph vielleicht die Ableitung einer der anderen Funktionen ist. Der Graph hat bei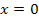 
eine Nullstelle und verläuft sonst immer oberhalb der x-Achse. Der Graph einer Funktion, die Abb. 2 als Ableitung besitzt, müsste somit bei 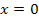eine waagrechte Tangente besitzen und sonst streng monoton steigend sein. So ein Graph ist in keiner der Abbildungen zu sehen. Also ist in Abb. 2 nicht der Graph einer Ableitungsfunktion der abgebildeten Funktionen zu sehen.
Nun zur Abb. 3. Hier ist sie noch einmal:
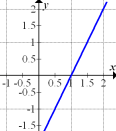
Abb. 3
Wir gehen wieder erst ´mal davon aus, dass wir den Graph einer Funktion 
vor uns haben. Es handelt sich um eine Gerade, d.h. die Steigung ist konstant. Die Ableitungsfunktion müsste eine waagrechte Gerade sein, doch so ein Graph ist in Abb. 1 bis 6. nicht dargestellt. Der in Abb. 3 gezeigte Graph kann daher nicht die Funktion selbst darstellen.
Aber vielleicht stellt der in Abb. 3 dargestellte Graph die Ableitung einer der anderen gezeigten Funktionen dar. Da bei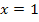 
eine Nullstelle mit Vorzeichenwechsel vorliegt, muss die zugehörige Funktion bei 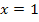ein Extremum haben, genauer gesagt einen Tiefpunkt. Weil für 
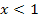der Graph in Abb. 3 unterhalb der x-Achse verläuft, muss die zugehörige Funktion hier fallen. Entsprechend muss der zugehörige Funktionsgraph für 
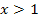steigen, da die in Abb. 3 gezeigte Gerade hier oberhalb der x-Achse liegt. Betrachte nun noch einmal die Abb. 1 bis 6 in der Angabe!
Unbedingt erst mal alleine nachdenken!
Auf was bist du gekommen?
Richtig! Nur Abb. 3 kann die Ableitungsfunktion von Abb. 5 sein.
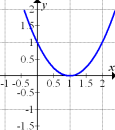
Abb. 5 |
Abb. 3 |
Nun zu Abb. 4, von der wir schon wissen, dass sie nicht die Ableitung der in Abb. 2 gezeigten Funktion ist. Hier noch einmal die Abbildung:
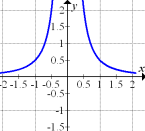
Abb. 4
Gehen wir wieder zuerst davon aus, dass wir hier den Graph der Funktion selbst vor uns haben. Da bei 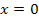eine Definitionslücke vorliegt, muss auch die Ableitungsfunktion hier eine Definitionslücke haben. Man kann eine Funktion schließlich nur dort ableiten, wo sie überhaupt definiert ist. (Wie sollte man denn auch die Steigung an einer Stelle angeben, wo gar kein Kurvenpunkt vorhanden ist?) Die einzige Abbildung, die sonst noch eine senkrechte Asymptote (Definitionslücke) bei 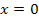hat, ist Abb. 6.
Betrachte dazu noch einmal Abb. 6:
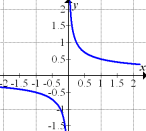
Abb. 6
Diese Abbildung kann aber nicht den Graph der Ableitung zur in Abb. 4 gezeigten Funktion darstellen, weil der Graph in Abb. 4 für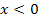 
steigt, so dass die Ableitungsfunktion oberhalb der x-Achse verlaufen müsste, was in Abb. 6 offensichtlich nicht der Fall ist.
