b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
So, nun weiter mit Abb. 2! Hier noch einmal der Graph.
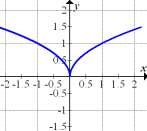
Abb. 2
Gehen wir bei unseren Überlegungen erst wieder davon aus, dass der gezeigte Graph die Funktion selbst darstellt. Da der Graph an der Stelle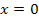 
eine Spitze hat, ist er hier nicht differenzierbar, d.h. die Steigung kann bei 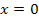nicht ermittelt werden. Die Tangente verläuft an dieser Stelle senkrecht;ihre Steigung kann nicht angegeben werden, weil sie ja unendlich großwäre. Der Graph der Ableitungsfunktion muss daher bei 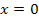eine Definitionslücke, genauer gesagt eine senkrechte Asymptote, besitzen. Die Ableitung nimmt schließlich in der Umgebung von 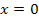vom Betrag her sehr große Werte an, denn die Tangenten an den Graph von Abb. 2 verlaufen nahezu senkrecht, wenn man sich von links bzw. von rechts beliebig nah an die Stelle 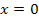annähert. Sie haben also vom Betrag her extrem hohe Steigungen. Deshalb geht dort die Steigung vom Betrag her gegen Unendlich, was letztendlich eben bedeutet, dass die Ableitungsfunktion bei 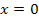eine senkrechte Asymptote haben muss.
Für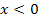 
, also links von der y-Achse, verläuft der in Abb.2 gezeigte Graph streng monoton fallend. Die zugehörige Ableitungsfunktion muss also für 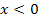unterhalb der x-Achse liegen. Umgekehrt steigt der dargestellte Graph für 
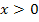, also rechts von der y-Achse, so dass die Ableitungsfunktion für 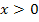oberhalb der x-Achse liegen muss.
Der in Abb. 2 dargestellte Graph hat keine waagrechten Tangenten;die zugehörige Ableitungsfunktion darf also keine Nullstellen haben.
Für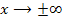 
, also ganz weit rechts bzw. links im Koordinatensystem, verläuft der gezeigte Graph immer flacher. Seine Steigung nähert sich an Null an, so dass sich die zugehörige Ableitungsfunktion an die x-Achse annähern muss. Nun betrachte noch einmal die Abb. 1 bis 6. Welche könnte nun die Ableitung zu dem in Abb. 2 gezeigten Graph sein?
Bitte wirklich erst einmal selber überlegen und dann erst weiterlesen!
Du hast hoffentlich erkannt, dass nur Abb. 6 in Frage kommt. Der in Abb. 6 gezeigte Graph ist die Ableitung des Graphen aus Abb. 2.
|
Abb. 2 |
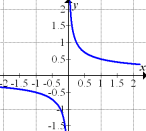
Abb. 6 |
Anmerkung:Der in Abb. 4 gezeigte Graph hat zwar bei 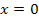ebenfalls eine senkrechte Asymptote, kann aber jedoch nicht die Ableitung des in Abb. 2 dargestellten Graphen sein, da der Graph in Abb. 4 für 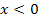oberhalb der x-Achse liegt. Die zugehörige Funktion müsste somit für 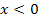streng monoton steigend sein, was bei Abb. 2 offensichtlich nicht der Fall ist.
Hier noch einmal zum Vergleich Abb. 2 und 4:
|
Abb. 2 |
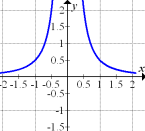
Abb. 4 Nicht die Ableitung zu Abb. 2 |
