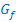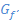b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
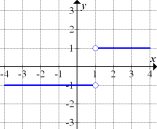
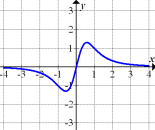
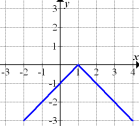
b.) Noch einmal dasselbe wie in a.) jedoch mit den Abbildungen 7 bis 12!
|
Abb. 7 |
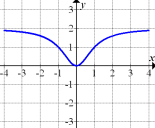
Abb. 8 |
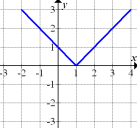
Abb. 9 |
|
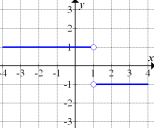
Abb. 10 |
Abb. 11 |
Abb. 12 |
Lösung:
Zu 4a.)
Wir betrachten die Abbildungen 1 bis 6. Das Problem ist, dass man nicht weiß, ob man bei einer bestimmten Abbildung den Graph der Funktion selbst oder den Graph ihrer Ableitungsfunktion vor sich hat. Wie der Angabe zu entnehmen ist, kann die Funktion, deren Graph in einer bestimmten Abbildung zu sehen ist, einerseits die Ableitungsfunktion zu einer anderen Abbildung sein als auch andererseits eine Funktion selbst, deren Ableitung dann gegebenenfalls in einer weiteren Abbildung zu sehen ist.
Um das Wirrwarr aus Funktionen und Ableitungsfunktionen zu entschlüsseln, gehen wir am besten systematisch vor:Wir beginnen mit Abb. 1 und denken uns den Graph der 1. Abbildung zuerst ´mal als Graph einer Funktion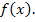 
Wie müsste der Graph ihrer Ableitungsfunktion aussehen? Hier noch einmal Abb. 1!
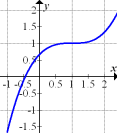
Abb. 1
Der Graph hat an der Stelle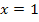 
eine waagrechte Tangente, ansonsten ist er streng monoton steigend. Der Graph der zugehörigen Ableitungsfunktion muss daher bei 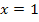eine Nullstelle ohne Vorzeichenwechsel (d.h. doppelte Nullstelle / Berührpunkt mit der x-Achse) haben und sonst oberhalb der x-Achse verlaufen. Nun schauen wir, welche der Abbildungen 2 bis 6 diese Anforderungen erfüllt. Betrachte dazu noch einmal die oben gezeigten Abbildungen! Offensichtlich kommt nur der in Abb. 5 gezeigte Graph in Frage.
Wie kann man sich noch zusätzlich versichern, dass Abb. 5 wirklich die Ableitung von Abb. 1 zeigt?
Der in Abb. 1 gezeigte Graph verläuft für große x-Werte immer steiler;die Steigung nimmt demnach für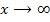 
immer mehr zu. D.h. die Werte der Ableitung müssen für 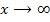immer größer werden. Der Graph der Ableitung muss steil nach rechts oben verlaufen. Für 
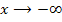fällt der in Abb. 1 gezeigte Graph immer stärker;die Steigung wird demnach für 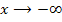immer negativer. D.h. die Werte der Ableitung werden dem entsprechend immer negativer. Der Graph der Ableitung muss steil nach links unten verlaufen. All dies ist bei Abb. 5 tatsächlich der Fall. Wir haben das erste Paar gefunden:Abb. 5 zeigt die Ableitung der in Abb.1 gezeigten Funktion.
|
Abb. 1 |
Abb. 5 |
Nun fragen wir uns umgekehrt, ob der in Abb. 1 gezeigte Graph vielleicht auch die Ableitung einer anderen dargestellten Funktion sein kann. Da der in Abb.1 gezeigte Graph ungefähr bei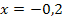 
eine Nullstelle mit Vorzeichenwechsel hat, müsste der zugehörige Funktionsgraph bei ungefähr 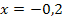ein Extremum besitzen. Keiner der in Abb. 2 bis 6 gezeigten Graphen erfüllt diese Bedingung, daher kann der in Abb. 1 gezeigte Graph nicht die Ableitung einer dieser Funktionen sein.
