b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

In der folgenden Abbildung sind zusätzlich zu den waagrechten Tangenten auch die beiden hier existierenden sogenannten Wendetangenten von dargestellt. Unter einer Wendetangente versteht man eine Tangente im Wendepunkt, also in einem Punkt, wo lokal am steilsten oder flachsten verläuft. Nicht wundern:An eine Wendetangente kommt der Graph von der einen Seite heran und geht von der anderen Seite wieder weg. (Bei anderen Tangenten kommt der Graph immer von einer Seite an die Tangente heran und geht von derselben Seite wieder weg.) Die Steigungen der Wendetangenten von entsprechen jeweils den y-Koordinaten der Extrema der Ableitungsfunktion .

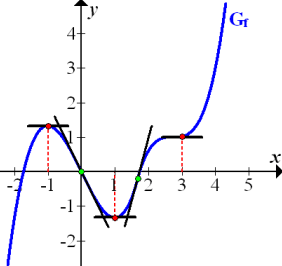
Abb.:Gegebener Graph mit waagrechten Tangenten und den beiden Wendetangenten;die Wendepunkte (das sind die Punkte, wo lokal am stärksten fällt bzw. steigt.) sind grün markiert.

Nun müsstest du in der Lage sein den Graph der Ableitungsfunktion zumindest grob zu skizzieren.

Verwende dabei die Nullstellen von x = -1 (einfache Nst.), x = 1 (einfache Nst.) und x = 3 (doppelt Nst. = TIP) sowie die beiden relativen Extrempunkte von , welche wir uns soeben überlegt haben:

TIP bei:T(0|-2) HOP bei:H(1,7|3,5)

Die Koordinaten dieser zwei Extrema sind zwar nur grobe Schätzungen, doch wir sollen den Graph der Ableitungsfunktion schließlich nur skizzieren. Für eine grobe Skizze reichen unsere Schätzungen allemal aus. (Eine exakte Zeichnung von lässt sich hier gar nicht machen.)

So, nun zeichne doch gleich ´mal selbst den Graph der gesuchten Ableitungsfunktion ohne vorher auf die folgende Abbildung zu schauen!

Hast du  inzwischen versucht zu skizzieren? Wenn nicht, dann bitte jetzt!

Hoffentlich hast du wirklich versucht alleine zu zeichnen. Dann kannst du deine Skizze jetzt mit der folgenden Abbildung vergleichen. Hier sind die beiden Graphen und in einem gemeinsamen Koordinatensystem dargestellt.

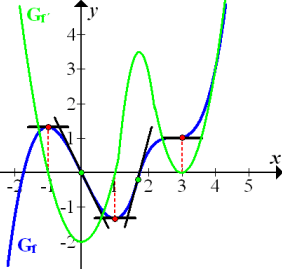
Abb.:Gegebener Graph in Blau mit Graph der Ableitungsfunktion in Grün

4. Bsp.:

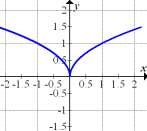
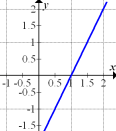
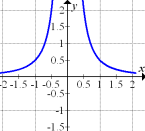
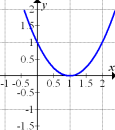
a.) In den Abbildungen 1 bis 6 sind die Graphen von Funktionen und ihren Ableitungsfunktionen wild durcheinander gemischt zu sehen. (Eine bestimmte Abbildung kann gegebenenfalls gleichzeitig sowohl den Graph einer Funktion selbst als auch die Ableitungsfunktion einer anderen darstellen.)

Ordne jeweils einem Funktionsgraphen den zugehörigen Graph der Ableitungsfunktion zu! Finde möglichst viele solcher Paare! Begründe deine Wahl.

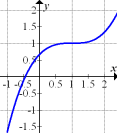
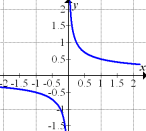
Abb. 1	Abb. 2	Abb. 3
Abb. 4	Abb. 5	Abb. 6

---