b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Jetzt fehlt uns noch der relative Hochpunkt der Ableitungsfunktion.
Der relative Hochpunkt der Ableitungsfunktion liegt genau an der Stelle, wo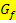 
relativ gesehen seine größte Steigung hat, also wo 
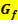zumindest innerhalb einer bestimmten Umgebung am steilsten ist.
Der relative Hochpunkt der Ableitungsfunktion 
hat somit die gleiche x-Koordinate wie derjenige Punkt auf der Funktion 
selbst, in dem am stärksten steigt. Die y-Koordinaten des Punktes auf 
und die y-Koordinate des jeweiligen Punktes auf 
sind in der Regel natürlich nicht gleich. Die y-Koordinate des Hochpunktes von entspricht ja der Tangentensteigung von an dieser Stelle. Es wäre reiner Zufall, wenn die y-Koordinate des Punktes auf den gleichen Wert hätte wie die Steigung an dieser Stelle. Nur dann wären neben den x-Koordinaten auch die y-Koordinaten der Punkte auf und gleich.
Versuche doch gleich mal selbständig am gegebenen Graphen abzulesen, an welcher Stelle er zumindest innerhalb eines bestimmten Bereichs am steilsten verläuft!
Es lässt sich leider nur ungefähr aus der gegebenen Zeichnung ablesen, an welcher Stelle der Funktionsgraph lokal am steilsten verläuft:Wir schätzen, dass dies bei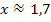 
der Fall ist. Wenn du selbst auf einen minimal abweichenden Wert z. B. 
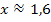oder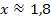 
gekommen bist, ist das auch ok. Wir gehen hier allerdings von 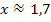aus. (Das ist ungefähr die x-Koordinate des grün markierten Punkts in der nächsten Abbildung.) Als nächstes zeichnen wir die Tangente an dieser Stelle ein und versuchen die Steigung so gut wie möglich abzulesen.
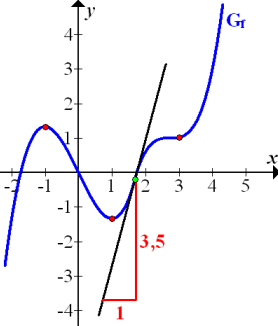
Abb.:Gegebener Graph mit Tangente im Punkt (1,7|?) und in Rot das zugehörige Steigungsdreieck. Im Punkt (1,7|?) steigt der Graph lokal am stärksten, seine Steigung ist daher an der Stelle x = 1,7 relativ gesehen am größten. Die Steigung der Tangente ist ungefähr 3,5 , weil beim Steigungsdreieck 1 nach rechts und ungefähr 3,5 nach oben gegangen wird.
Wir schätzen hier also, dass die Steigung bei x = 1,7 ungefähr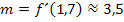 
ist. Dies entspricht der y-Koordinate des Hochpunktes von . (Die Ableitungsfunktion ordnet ja jedem x den Wert der Steigung von an dieser Stelle zu.) Die Ableitungsfunktion hat demnach ihren relativen Hochpunkt ungefähr bei (1,7|3,5).
Hochpunkt der Ableitungsfunktion:H(1,7|3,5)
Punkte, wo der Funktionsgraph lokal am steilsten bzw. flachsten verläuft, heißen übrigens Wendepunkte von . In diesen Punkten ändert sich die sogenannte Krümmung des Graphen.
Du kannst die Punkte, wo der Funktionsgraph lokal am steilsten bzw. flachsten verläuft, (also die Wendepunkte) daher auch folgendermaßen finden:Stell dir vor, du würdest von links nach rechts zum Beispiel mit einem Fahrrad auf dem Funktionsgraphen entlang fahren. Die Wendepunkte liegen dort, wo du den Lenker des Fahrrads von links nach rechts oder umgekehrt umlenkst. Genauer wird darauf erst später im Teil Zweite Ableitung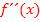 
eingegangen, dort wird auch die Berechnung der Wendepunkte erklärt. Doch das führt momentan noch zu weit.
