b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Um den Zusammenhang zwischen Steigungsverhalten von 
und Verlauf des Graphen 
der Ableitungsfunktion für dich übersichtlicher zu gestalten, werden nun die soeben besprochenen Zusammenhänge in Form einer Tabelle dargestellt.
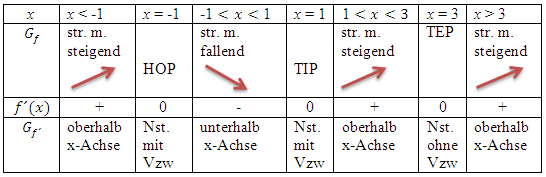
Erläuterung der verwendeten Abkürzungen:
Die Abkürzung „str. m.“ (steigend bzw. fallend) steht für „streng monoton“ (steigend bzw. fallend).
Die Abkürzung „Vzw“ steht für „Vorzeichenwechsel“.
„Nst.“ ist, wie du wahrscheinlich selbst weißt, die Abkürzung für „Nullstelle“.
Diese Abkürzungen sind auch allgemein gebräuchlich. Du wirst noch öfter auf sie stoßen, nicht nur auf dieser website.
Neben den Nullstellen der Ableitungsfunktion sind für uns auch besonders ihre Extrema von Interesse. Vorsicht:Es geht um die Extrema der Ableitung und nicht um die Extrema der Funktion 
! Ganz genau kann man sie hier nicht auf sie kommen, nur ungefähr. Doch das Prinzip soll kurz erklärt werden.
Um einen relativen Tiefpunkt der Ableitungsfunktion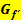 
zu ermitteln, muss man sich überlegen, an welcher Stelle die Steigung von 
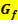ihr lokales Minimum annimmt, also wo 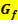zumindest innerhalb einer bestimmten Umgebung am stärksten fällt.
Das ist hier ziemlich genau bei x = 0, weil der Graph dort am stärksten fällt. Ganz exakt kann man das nicht aus der Zeichnung ablesen. Die y-Koordinate des Kurvenpunktes (0|0) von ist für den Verlauf der Ableitungsfunktion nicht relevant. Was für aber sehr wohl wichtig ist, ist die Steigung von bei x = 0. Sie lässt sich hier leider nur grob abschätzen:Man zeichnet dazu so genau wie möglich in die gegebene Zeichnung bei x = 0 die Tangente an ein und liest dann mit Hilfe eines Steigungsdreiecks die Steigung dieser Tangente ab. Betrachte dazu die nächste Abbildung! Dort ist die erwähnte Tangente im Punkt (0|0) zu sehen.
Wir schätzen die Tangentensteigung bei x = 0 hier ´mal grob mit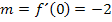 
ab. Dieser Wert der Tangentensteigung von 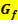entspricht der y-Koordinate des Tiefpunktes von 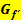. (Die Ableitungsfunktion ordnet ja jedem x den Wert der Steigung von an dieser Stelle zu.) Somit muss der Tiefpunkt der Ableitungsfunktion ungefähr bei (0|-2) liegen.
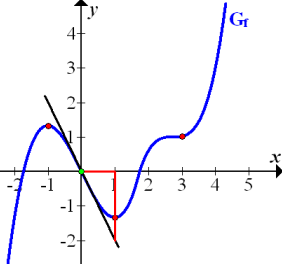
Abb.:Gegebener Graph mit Tangente im Punkt (0|0) und in Rot das zugehörige Steigungsdreieck. Im Punkt (0|0) fällt der Graph lokal am stärksten, seine Steigung ist daher an der Stelle x = 0 relativ gesehen am kleinsten. Die Steigung der Tangente ist ungefähr -2 , weil beim Steigungsdreieck 1 nach rechts und 2 nach unten gegangen wird.
Tiefpunkt der Ableitungsfunktion:T(0|-2)
