b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)

Merke: Waagrechte Tangente ⇔ Steigung = 0 ⇔

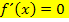
Im Folgenden noch einmal die Abbildung. Zusätzlich sind die waagrechten Tangenten in Schwarz (fett) eingezeichnet. Die gestrichelten Linien sollen es dir vereinfachen, die jeweiligen x-Koordinaten der Punkte mit waagrechten Tangenten abzulesen.

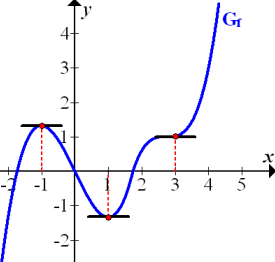
Aus der Abbildung lässt sich gut ablesen:

Relativer Hochpunkt bei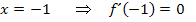

Relativer Tiefpunkt bei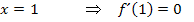

Terrassenpunkt bei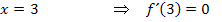

Daher muss die Ableitungsfunktion die Nullstellen x = -1, x = 1 und x = 3 haben.

Bei x = -1 und x = 1 hat jeweils einen relativen Extrempunkt. Das Vorzeichen der Steigung von ändert sich jeweils an diesen Stellen. Zuerst steigt der Graph schließlich, dann fällt er bzw. umgekehrt. D.h. das Vorzeichen der Ableitung ändert sich jeweils an diesen Stellen;die Ableitungsfunktion hat dort Nullstellen mit Vorzeichenwechsel, also einfache Nullstellen.

Der Graph der Ableitungsfunktion muss deswegen die x-Achse bei x = -1 und x = 1 schneiden. (Bei einfachen Nullstellen wird die x-Achse immer geschnitten;bei doppelten Nullstellen berührt der Graph dagegen die x-Achse nur, schneidet aber nicht. Mehr dazu bei:Vielfachheiten der Nullstellen)

Bei x = 3 hat einen Terrassenpunkt. Im Terrassenpunkt von verläuft die Tangente an waagrecht, die Tangentensteigung und somit auch die y-Koordinate des Punktes bei x = 3 auf der Ableitungsfunktion muss gleich 0 sein. Nullstelle der Ableitungsfunktion N(3|0)

Etwas links vom Terrassenpunkt steigt , verläuft direkt im Terrassenpunkt kurz waagrecht und steigt dann wieder weiter. Die Steigung von ist deshalb zuerst positiv, dann Null und danach wieder positiv. Sie ändert ihr Vorzeichen an der Stelle x = 3 nicht! Dies bedeutet, dass die Ableitung zuerst positiv, dann gleich Null und nachher wieder positiv ist. Es gibt also keinen Vorzeichenwechsel der Ableitungsfunktion an der Stelle x = 3. Die Ableitungsfunktion muss bei x = 3 eine Nullstelle ohne Vorzeichenwechsel, also eine doppelte Nullstelle besitzen.

Weil der Funktionsgraph links und rechts in der Umgebung des Terrassenpunktes steigt, ist die Ableitung etwas links bzw. rechts von x = 3 positiv. Das heißt, dass die y-Koordinaten der Punkte auf der Ableitungsfunktion in der näheren Umgebung von x = 3 positiv sein müssen. Daher liegen diese Punkte zwangsläufig oberhalb der x-Achse. Wir folgern daraus:Der Graph der Ableitungsfunktion muss für 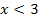von oben an die x- Achse herankommen, muss sie dann kurz bei x = 3 berühren und danach wieder oberhalb der x-Achse weitergehen.

---