b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Nach diesen Überlegungen können wir den Graph einer Funktion  zu unserer Ableitungsfunktion zeichnen. Versuche es doch einmal alleine, ohne dir die nächste Abbildung anzuschauen!
zu unserer Ableitungsfunktion zeichnen. Versuche es doch einmal alleine, ohne dir die nächste Abbildung anzuschauen!
Wenn du alles richtig gemacht hast, sieht dein Graph von der Form her aus wie der in der folgenden Abbildung gezeigte Graph  . Dein Funktionsgraph kann natürlich im Vergleich zu diesem Graph beliebig nach oben oder unten verschoben sein. Das haben wir ja schon besprochen. (Von
. Dein Funktionsgraph kann natürlich im Vergleich zu diesem Graph beliebig nach oben oder unten verschoben sein. Das haben wir ja schon besprochen. (Von  lässt sich ohne weitere Angaben nicht eindeutig auf
lässt sich ohne weitere Angaben nicht eindeutig auf  schließen.)
schließen.)
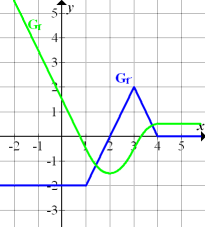
Wir fassen noch einmal alles Wichtige zusammen, was du an diesem Beispiel lernen solltest:
Der Funktionswert der Ableitungsfunktion, also die y-Koordinate eines Punktes 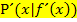 , der auf dem Graph der Ableitungsfunktion
, der auf dem Graph der Ableitungsfunktion 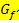 liegt, gibt die Steigung der Funktion
liegt, gibt die Steigung der Funktion 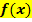 an der Stelle x an.
an der Stelle x an.
Ist der Graph der Ableitungsfunktion 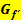 eine waagrechte Gerade, so ist der Graph der Funktion
eine waagrechte Gerade, so ist der Graph der Funktion 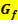 eine schräge Gerade, da die Ableitung konstant ist und somit die Steigung von
eine schräge Gerade, da die Ableitung konstant ist und somit die Steigung von  ebenfalls konstant sein muss. Ist die Steigung einer Funktion
ebenfalls konstant sein muss. Ist die Steigung einer Funktion  konstant, kann es sich bei
konstant, kann es sich bei  nur um eine Gerade handeln.
nur um eine Gerade handeln.
Ist der Graph der Ableitungsfunktion 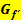 eine schräge Gerade, so ist Graph der Funktion
eine schräge Gerade, so ist Graph der Funktion 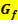 eine Parabel.
eine Parabel.
Wo 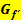 unterhalb der x-Achse verläuft, ist die Ableitung, d.h. die Steigung von
unterhalb der x-Achse verläuft, ist die Ableitung, d.h. die Steigung von  , negativ und
, negativ und 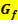 fällt.
fällt.
Wo 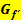 oberhalb der x-Achse verläuft, ist die Ableitung, d.h. die Steigung von
oberhalb der x-Achse verläuft, ist die Ableitung, d.h. die Steigung von  , positiv und
, positiv und 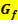 steigt.
steigt.
Wo 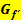 eine Nullstelle hat, ist die Ableitung gleich Null, so dass
eine Nullstelle hat, ist die Ableitung gleich Null, so dass 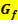 an dieser Stelle eine waagrechte Tangente hat. Das ergibt die x-Koordinate des Scheitels der Parabel
an dieser Stelle eine waagrechte Tangente hat. Das ergibt die x-Koordinate des Scheitels der Parabel  .
.
In der soeben vorgeführten Aufgabe musste (soweit möglich) vom Graph  auf den Funktionsgraphen
auf den Funktionsgraphen  geschlossen werden. Da
geschlossen werden. Da  eine Stammfunktion von
eine Stammfunktion von  ist, entspricht die Aufgabenstellung vom
ist, entspricht die Aufgabenstellung vom  auf
auf  zu schließen im Prinzip dem Problem vom Funktionsgraph
zu schließen im Prinzip dem Problem vom Funktionsgraph  auf den Graph ihrer Stammfunktion
auf den Graph ihrer Stammfunktion 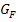 zu schließen, da für eine Stammfunktion
zu schließen, da für eine Stammfunktion 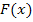 zu einer Funktion
zu einer Funktion  schließlich gilt:
schließlich gilt: 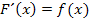
Zusammenhang zwischen Funktionsgraph 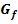 und Graph und Graph 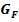 einer Stammfunktion: einer Stammfunktion:
Merke:
· Bei den x-Koordinate, wo · An der Stelle, wo · An der Stelle, wo · In den Bereichen, wo · In den Bereichen, wo Es gibt zu einer Funktion Soll zu einem gegebenen Graph |

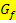
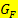
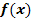 unendlich viele verschiedene Stammfunktionen
unendlich viele verschiedene Stammfunktionen 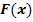 . Die Stammfunktionen unterscheiden sich nur in einer additiven Konstante C, d.h. in einer Zahl, die zu
. Die Stammfunktionen unterscheiden sich nur in einer additiven Konstante C, d.h. in einer Zahl, die zu 