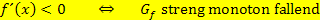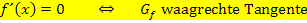b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f´(x)
Im Folgenden wollen wir uns ausführlich mit den Zusammenhängen einer Funktion 
mit ihrer Ableitungsfunktion 
beschäftigen.
Weil das Wort „Ableitungsfunktion“ so lang ist, werden wir im Folgenden auch oft nur von der „Ableitung“ 
reden. Das ist auch allgemein üblich. Dass da eigentlich ein Unterschied ist zwischen der Ableitungsfunktion und der Ableitung 
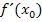an einer bestimmten Stelle, ist dir hoffentlich klar. Wenn nicht, gehe zu Unterschied zwischen Ableitung 
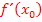an einer bestimmten Stelle 
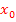und Ableitungsfunktion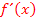 
Also, wie hängen nun die Funktion und ihre Ableitung zusammen? Du weißt bisher:Mit der Ableitung kann man die Steigung einer Kurve berechnen. entspricht bei Kurven praktisch der Steigung m von Geraden.
Wenn m positiv ist, steigt eine Gerade streng monoton. Entsprechend ist eine Kurve streng monoton steigend, wenn positiv ist.
Ist die Steigung m einer Geraden negativ, fällt die Gerade streng monoton. Entsprechend ist ein Funktion streng monoton fallend, wenn negativ ist.
Für m = 0 verläuft eine Gerade waagrecht, daher verläuft die Tangente an eine Funktion waagrecht, wenn 
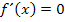ist.
| Zusammenfassung:
|
Zusammenhang der Graphen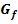 
und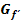 
Wichtig:Die Steigung der Funktion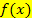 
an einer bestimmten Stelle 
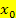entspricht dem y-Wert der Ableitungsfunktion 
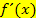an dieser Stelle 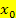. Du erhältst demnach die y-Koordinate eines Punktes 
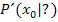auf der Ableitungsfunktion, indem du die Tangentensteigung von an der Stelle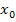 
nimmst. Du gehst also zu einem Punkt P auf dem Graphen von , zeichnest dort die Tangente an den Funktionsgraph 
und liest die Steigung der Tangente ab. Der Wert der Tangentensteigung von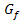 
entspricht der y-Koordinate des Punktes P´auf der Ableitungsfunktion. P und P´haben dabei natürlich die gleiche x-Koordinate. Die „Höhe“ des Punktes P´auf dem Graph der Ableitungsfunktion hängt also nur von der Steigung der Funktion im Punkt P ab.
· Wenn der Graph 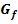streng monoton fallend ist, ist die Tangentensteigung und somit die Ableitung 
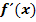negativ, was bedeutet, dass die y-Koordinate eines Punktes P´der Ableitungsfunktion negativ ist und P´daher unterhalb der x-Achse liegt. Daher verläuft der Graph der Ableitungsfunktion 
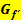unterhalb der x-Achse, wo 
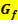streng monoton fallend ist.
· Ist der Graph 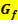streng monoton steigend, ist die Ableitung positiv, so dass der Graph der Ableitungsfunktion 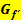oberhalb der x-Achse verläuft. Wo der Graph 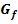streng monoton steigend ist, ist die Tangentensteigung und somit die Ableitung 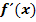positiv, was bedeutet, dass die y-Koordinate eines Punktes P´der Ableitungsfunktion positiv ist und P´daher oberhalb der x-Achse liegt.
· Wo der Graph 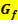eine waagrechte Tangente hat, hat der Graph der Ableitungsfunktion 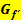eine Nullstelle. Hat der Graph eine waagrechte Tangente, ist die Tangentensteigung von gleich 0 ist. Die Tangentensteigung von entspricht der y-Koordinate der Punkte P´auf der Ableitungsfunktion . Daher ist die y-Koordinate eines Punktes P´gleich 0, wenn dort eine waagrechte Tangente, also die Steigung 0, hat. Bekanntlich liegt ein Punkt mit der y-Koordinate y = 0 auf der x-Achse und somit ist P´eine Nullstelle der Ableitungsfunktion . Deshalb hat der Graph der Ableitungsfunktion 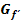eine Nullstelle, wo der Graph 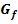eine waagrechte Tangente hat.
