a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Einsetzen von 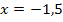 in
in 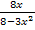 ergibt:
ergibt:
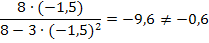
Einsetzen von 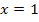 in
in 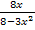 ergibt:
ergibt:
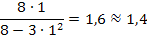
An der Stelle x = -1,5 ergibt sich definitiv ein ganz anderer Wert als -0,6. Obwohl beim Einsetzen von x = 1 ein ungefahr passender Wert herauskommt, kann 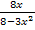 deshalb nicht der Term der Ableitungsfunktion
deshalb nicht der Term der Ableitungsfunktion  sein.
sein.
Dann wird wohl 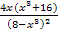 die Ableitungsfunktion von
die Ableitungsfunktion von 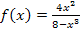 sein. Zur Kontrolle setzen wir aber auch noch in
sein. Zur Kontrolle setzen wir aber auch noch in 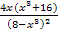 die Zahlen x = -1,5 und x = 1 ein.
die Zahlen x = -1,5 und x = 1 ein.
Einsetzen von 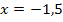 in
in 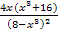 ergibt:
ergibt:
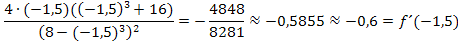
Einsetzen von 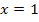 in
in 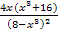 ergibt:
ergibt:
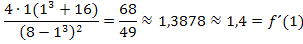
Die berechneten Werte stimmen beide jeweils recht gut mit den graphisch ermittelten Naherungswerten 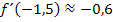 und
und 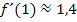 uberein. Deshalb muss gelten:
uberein. Deshalb muss gelten:
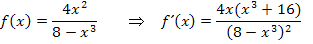
Die Ableitungsfunktion zu f (x) ist also 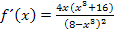 und nicht
und nicht 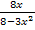 .
.
Zu 4c.)
Gesucht ist hier die Gleichung der Tangente an 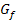 an der Stelle x = 1. Es soll dabei auf 2 Nachkommastellen gerundet werden. Eine Tangente ist eine lineare Funktion / Gerade;sie hat also die allgemeine Gleichung:
an der Stelle x = 1. Es soll dabei auf 2 Nachkommastellen gerundet werden. Eine Tangente ist eine lineare Funktion / Gerade;sie hat also die allgemeine Gleichung: 
Die Steigung m entspricht der Ableitung 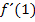 . D.h. m ist bereits aus Teilaufgabe 4b. bekannt, denn dort haben wir
. D.h. m ist bereits aus Teilaufgabe 4b. bekannt, denn dort haben wir 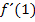 im Prinzip schon berechnet.
im Prinzip schon berechnet.
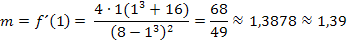
Um den y-Achsenabschnitt t berechnen zu konnen, benotigen wir au?erdem die y-Koordinate des Kurvenpunktes (1| f (1)). Wir berechnen sie durch Einsetzen von x = 1 in 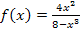 .
.
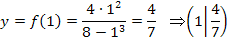
Jetzt konnen wir den y-Achsenabschnitt t berechnen. Dazu setzen wir die Koordinaten des Kurvenpunktes 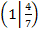 und den berechneten Wert von m in die allgemeine Geradengleichung
und den berechneten Wert von m in die allgemeine Geradengleichung  ein und losen anschlie?end nach t auf. Dabei rechnen wir mit den exakten Werten und runden erst am Ende der Rechnung.
ein und losen anschlie?end nach t auf. Dabei rechnen wir mit den exakten Werten und runden erst am Ende der Rechnung.
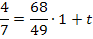
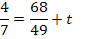
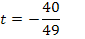
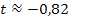
Die Gleichung der gesuchten Tangente lautet somit: 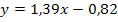
Zu 4d.)
Gesucht ist der Winkel, unter dem die in 4c. berechnete Tangente die x-Achse schneidet, also der Neigungswinkel dieser Tangente. Die Steigung der Tangente haben wir bereits in Teilaufgabe 4b. bzw. 4c. berechnet: 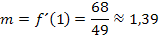
Wir setzen den exakten Wert von m in die Formel 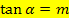 ein und berechnen mit dem Taschenrechner den gesuchten Winkel
ein und berechnen mit dem Taschenrechner den gesuchten Winkel 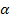 . (Der Taschenrechner muss dabei auf Mode DEG eingestellt sein, weil wir schlie?lich einen Winkel im Gradma?und nicht im Bogenma? suchen. Tastenfolge:shift tan
. (Der Taschenrechner muss dabei auf Mode DEG eingestellt sein, weil wir schlie?lich einen Winkel im Gradma?und nicht im Bogenma? suchen. Tastenfolge:shift tan 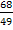 )
)
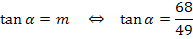
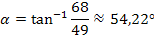
Damit ist die Aufgabe gelost. Fertig!
Weitere Aufgaben zu Berechnungen mit  und alles zum Zusammenhang der Graphen
und alles zum Zusammenhang der Graphen 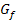 und
und 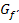 findest du im Teil b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f ´(x)
findest du im Teil b.) Zusammenhang der Funktion f (x) mit ihrer Ableitungsfunktion f ´(x)
- Page 9 of 9
- « Previous
- 6
- 7
- 8
- 9
- Next »

