a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Daher muss ihre Steigung negativ sein. Aus der Lange der senkrechten Strecke, in diesem Fall mit negativem Vorzeichen, ergibt sich die gesuchte Steigung an der Stelle x = -1,5. Das Ergebnis entspricht der Ableitung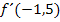 
.
An der Stelle x = 1 gehst du dann entsprechend vor:Tangente mit Steigungsdreieck im Kurvenpunkt (1|f (1)) einzeichnen und Steigung ablesen. Das Ergebnis entspricht der Ableitung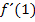 
.
Deine Zeichnung sollte im Prinzip aussehen wie die folgende Abbildung.
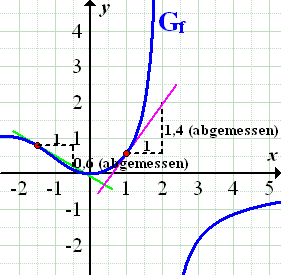
Abb.:Graph 
der Funktion 
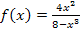mit den Tangenten samt Steigungsdreieck an den Stellen x = -1,5 und x = 1
Aus der Zeichnung ist zu entnehmen:
Die Steigung der Tangente an 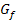im Punkt (-1,5|f (-1,5)) ist ungefahr -0,6;die Steigung der Tangente im Punkt (-1,5|f (-1,5)) ist ungefahr 1,4. Somit gilt fur die Ableitung von f :
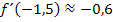
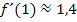
Dies sind naturlich nur grobe Naherungswerte, denn ganz genau lassen sich die Tangenten ohne Rechnung logischerweise nicht einzeichnen. Au?erdem haben wir ihre Steigungen blo?durch Abmessen ermittelt und ganz exakt messen kann man eben nicht. Falls du selbst also auf minimal abweichende Werte gekommen bist, ist das nicht schlimm. Es kommt hier vor allem auf das Prinzip an. Eine Abweichung der Ergebnisse von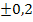 
liegt hier absolut im Rahmen. Wenn du selbst beispielsweise auf 
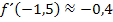oder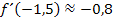 
gekommen bist, wird das noch als korrekt gewertet. Viel ungenauer sollten die Ergebnisse jedoch nicht sein.
Zu 4b.)
Es soll mit Hilfe der Ergebnisse von Teilaufgabe 4a. herausgefunden werden, ob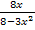 
oder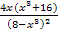 
der Funktionsterm der Ableitungsfunktion ist. Es ist also die Frage zu beantworten, ob 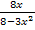oder 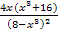die Ableitungsfunkti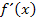on 
von 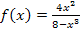ist.
Das lasst sich folgenderma?en entscheiden:Aus 4a. wissen wir zumindest ungefahr die Werte der Ableitung f ? an den Stellen x = -1,5 und x = 1:
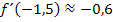
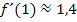
Wenn 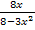der Funktionsterm der Ableitungsfunktion 
ist, mussten sich beim Einsetzen von x = -1,5 und x = 1 ungefahr die Werte -0,6 bzw. 1,4 ergeben. (Durch das Einsetzen der jeweiligen x-Koordinate in erhalt man bekanntlich genau die Steigung der Funktion 
bzw. die Tangentensteigung an der entsprechenden Stelle.) Wenn ganz andere Ergebnisse beim Einsetzen von x = -1,5 und x = 1 in 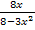herauskommen, wird wohl der andere angegebene Term 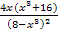die Ableitungsfunkti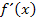on von 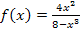sein. Zur Sicherheit setzt du aber auch noch in 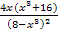die Zahlen x = -1,5 und x = 1 ein und vergleichst wieder mit den Ergebnissen aus 4a.
Du musst also nur jeweils die Zahlen x = -1,5 und x = 1 in die beiden angegebenen Terme 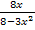und 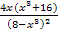einsetzen und schauen, bei welchem sich dabei ungefahr die Werte -0,6 bzw. 1,4 ergeben.
