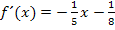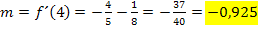a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)

Hinweis:

Manchmal ist beim Aufgabentyp 2 die Tangentensteigung m nicht direkt angegeben, sondern versteckt in der Steigung einer parallelen Geraden oder in der Angabe des Schnittwinkels 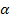der Tangente mit der x-Achse oder einer anderen waagrechten Geraden. Von diesem Winkel 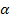kommt man mit der folgenden Formel ganz leicht auf m.

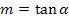
Und nun noch zwei abschlie?ende Beispiele. Probiere es zuerst alleine die nachsten beiden Aufgaben zu losen, bevor du dir jeweils die Losung anschaust! Wenn du wirklich alles verstanden hast, musstest du auch alleine auf die Losungen kommen. Daran kannst du deine Kenntnisse betreffs der Ableitungsfunktion gut selber testen.

3. Bsp.:Aufgabe aus einer 1. Schulaufgabe 11. Klasse G8

Gegeben ist die Funktion f mit der Gleichung 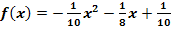. Ihr Graph 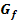beschreibt im Bereich 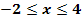eine Kurve, die eine Schlittschuhlauferin in einem Eisstadion durchlauft. (Vergleiche Abbildung!) Bei x = 4 sturzt die Eislauferin und rutscht ab dieser Stelle geradlinig weiter.

a.) Berechne die Gleichung der Geraden g, entlang derer die Eislauferin nach ihrem Sturz weiterrutscht.

b.) Die Gerade x = 5 entspricht der Au?enwand der Eisflache. Unter welchem spitzen Winkel 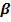prallt die ungluckliche Eislauferin gegen diese Wand?

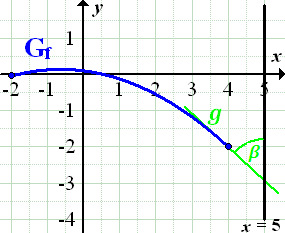
Abb.:Graph 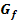der Funktion 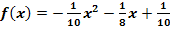im Intervall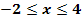

Losung:

Zu 3a.)

Der Knackpunkt dieser Aufgabe liegt in der Tatsache, dass die Eislauferin nach ihrem Sturz bei x = 4 naturlich tangential zu ihrer ursprunglichen Laufkurve 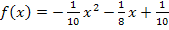weiterrutscht.

Die gesuchte Gerade g entspricht daher der Tangente an den Graphen 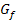der gegebenen Funktion 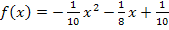an der Stelle x = 4. Du musst also einfach die Gleichung der Tangente an 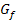an der Stelle x = 4 berechnen. Eine Tangente ist logischerweise eine lineare Funktion / Gerade;sie hat also allgemein die Gleichung:

Die Steigung m entspricht der Ableitung .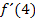

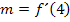
Um 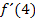zu berechnen, leitest du 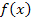erst einmal mit den Ableitungsregeln ab;das ergibt dann die Gleichung der Ableitungsfunktion 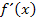. In die Ableitungsfunktion setzt du dann die gegebene x-Koordinate x = 4 ein;dadurch erhaltst du die gesuchte Steigung m der Tangente an dieser Stelle. Das kannst du bestimmt alleine. Also gleich ?mal selbst ausrechnen, wenn du es noch nicht gemacht hast!

Zu deiner Kontrolle:

Gegebene Funktion: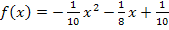
Ableitungsfunktion: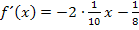
Steigung an der Stelle x = 4: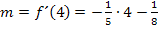

Hinweis:Man hatte m naturlich auch mit dem Differenzialquotienten berechnen konnen, doch das ware viel zu umstandlich.

---