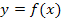a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Wie findet man also den Punkt P bzw. seine x-Koordinate, wenn man nur die Tangentensteigung m in diesem Punkt und die Funktionsgleichung  kennt? Ganz einfach:Man bildet erst einmal
kennt? Ganz einfach:Man bildet erst einmal  und setzt
und setzt  mit der gegebenen Tangentensteigung m gleich. Es gilt schlie?lich:
mit der gegebenen Tangentensteigung m gleich. Es gilt schlie?lich: 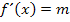
So ergibt sich eine Gleichung mit der Unbekannten x, die du nur noch nach x auflosen brauchst und schon hast du die gesuchte x-Koordinate des Punktes P berechnet. Die y-Koordinate von P erhaltst du durch Einsetzen der berechneten x-Koordinate in die Funktionsgleichung  .
.
2. Bsp.:
In welchem Punkt P verlauft die Tangente an die Funktion 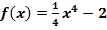 parallel zu der Geraden
parallel zu der Geraden 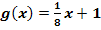 ?
?
Losung:
Zwei Geraden sind genau dann parallel, wenn sie die gleiche Steigung haben. Die Tangente soll parallel zu 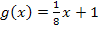 verlaufen, daher mussen die Tangente und die Gerade g die gleiche Steigung besitzen. Weil die Gerade g die Steigung
verlaufen, daher mussen die Tangente und die Gerade g die gleiche Steigung besitzen. Weil die Gerade g die Steigung 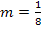 hat, muss auch die Tangente die Steigung
hat, muss auch die Tangente die Steigung 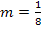 haben. Wir kennen somit die Tangentensteigung und suchen den zugehorigen Punkt P auf der Funktion
haben. Wir kennen somit die Tangentensteigung und suchen den zugehorigen Punkt P auf der Funktion 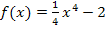 .
.
Wir bilden erst einmal die Ableitung: 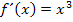
Nun setzen wir die Ableitung mit 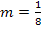 gleich:
gleich:
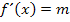
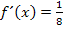

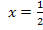
Das ist schon die x-Koordinate von P. Nun fehlt nur noch die y-Koordinate von P. Wir erhalten sie durch Einsetzen von 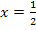 in die Funktionsgleichung
in die Funktionsgleichung 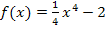 .
.
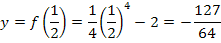
Der gesuchte Punkt hat somit die Koordinaten: 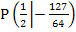
| Zusammenfassung:
Aufgabentyp 1: Die x-Koordinate eines Kurvenpunktes P von Geg.: Ges.: Steigung der Funktion im Punkt P / Tangentensteigung m Losung:
D.h. x-Koordinate von P einsetzen in Aufgabentyp 2: Es ist die Steigung der Funktion bzw. die Tangentensteigung m gegeben und die x-Koordinate des zugehorigen Kurvenpunktes ist gesucht. Dann musst du die gegebene Steigung m mit der Ableitung Geg.: Ges.: x-Koordinate des Beruhrpunktes P von Tangente und Funktion Losung:
D.h. Ableitung Falls die y-Koordinate von P auch noch gesucht ist, musst du die ermittelte x-Koordinate in die Funktionsgleichung
|

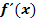 einsetzen! So bekommst du die gesuchte Tangentensteigung.
einsetzen! So bekommst du die gesuchte Tangentensteigung.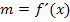
 Tangentensteigung m
Tangentensteigung m