a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Kurze Wiederholung: Steigung m von Geraden
Bei Geraden in der Form 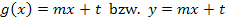 wird die Steigung mit m bezeichnet. Soll eine Gerade mit Hilfe von m und t gezeichnet werden, zeichnet man ausgehend vom y-Achsenabschnitt t auf der y-Achse ein Steigungsdreieck. Dazu stellt man sich m als Bruch vor;den Nenner geht man von t aus immer nach rechts und den Zahler nach oben, wenn m positiv ist, bzw. nach unten, wenn m negativ ist. Es gilt:
wird die Steigung mit m bezeichnet. Soll eine Gerade mit Hilfe von m und t gezeichnet werden, zeichnet man ausgehend vom y-Achsenabschnitt t auf der y-Achse ein Steigungsdreieck. Dazu stellt man sich m als Bruch vor;den Nenner geht man von t aus immer nach rechts und den Zahler nach oben, wenn m positiv ist, bzw. nach unten, wenn m negativ ist. Es gilt:
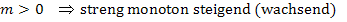
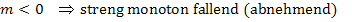
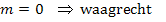
Bei einer bestimmten Gerade ist die Steigung m immer eine feste Zahl. Die Steigung einer Geraden ist konstant, d.h. sie andert sich nicht. Egal, an welcher Stelle man sich auf der Geraden befindet, die Steigung m ist immer gleich. Sonst ware es ja keine Gerade. Sobald sich die Steigung andert, entsteht schlie?lich eine Kurve, die teils flacher und teils steiler verlauft.
Ist der Graph einer Funktion  keine Gerade, sondern eine Kurve, hangt die Steigung der Funktion immer vom jeweiligen Kurvenpunkt ab. Ein Kurvenpunkt P ist durch seine x-Koordinate eindeutig festgelegt, denn seine y-Koordinate kann ja durch Einsetzen seiner x-Koordinate in die Funktionsgleichung
keine Gerade, sondern eine Kurve, hangt die Steigung der Funktion immer vom jeweiligen Kurvenpunkt ab. Ein Kurvenpunkt P ist durch seine x-Koordinate eindeutig festgelegt, denn seine y-Koordinate kann ja durch Einsetzen seiner x-Koordinate in die Funktionsgleichung  leicht berechnet werden. Fur jeden Kurvenpunkt von
leicht berechnet werden. Fur jeden Kurvenpunkt von 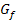 gilt ja
gilt ja 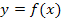 . Es reicht somit vollig aus, nur die x-Koordinate des jeweiligen Kurvenpunktes zu kennen, um die Steigung der Funktion
. Es reicht somit vollig aus, nur die x-Koordinate des jeweiligen Kurvenpunktes zu kennen, um die Steigung der Funktion 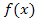 an dieser Stelle eindeutig berechnen zu konnen. Die Steigung der gesamten Kurve ist allerdings keine konstante Zahl, sondern ein mathematischer Ausdruck, der von x abhangt. Wir schreiben bei einer Funktion
an dieser Stelle eindeutig berechnen zu konnen. Die Steigung der gesamten Kurve ist allerdings keine konstante Zahl, sondern ein mathematischer Ausdruck, der von x abhangt. Wir schreiben bei einer Funktion  fur die Steigung anstatt m daher
fur die Steigung anstatt m daher  . Das x in der Klammer weist auf die Abhangigkeit von x hin. Nur wenn man x kennt, kann man die Steigung konkret als Zahl angeben.
. Das x in der Klammer weist auf die Abhangigkeit von x hin. Nur wenn man x kennt, kann man die Steigung konkret als Zahl angeben.
Also noch einmal, weil es so wichtig ist:
Wenn du die Steigung einer Kurve berechnen willst, musst du die x-Koordinate des jeweiligen Kurvenpunktes in die Ableitungsfunktion 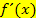 einsetzen. Dadurch erhaltst du die konkrete Steigung an dieser Stelle.
einsetzen. Dadurch erhaltst du die konkrete Steigung an dieser Stelle.
1. Bsp.:
Gegeben ist die Funktion 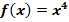 . Im Punkt
. Im Punkt 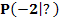 wird die Tangente an
wird die Tangente an 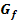 gelegt. Berechne die Tangentensteigung!
gelegt. Berechne die Tangentensteigung!
Losung:
Um die Steigung der Tangente an die Funktion 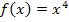 im Kurvenpunkt P(-2|?) zu ermitteln, muss man zuerst die Ableitungsfunktion
im Kurvenpunkt P(-2|?) zu ermitteln, muss man zuerst die Ableitungsfunktion  bilden und in diesen Ausdruck fur x die gegebene x-Koordinate -2 einsetzen.
bilden und in diesen Ausdruck fur x die gegebene x-Koordinate -2 einsetzen.
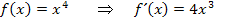
Steigung der Tangente im Kurvenpunkt P(-2|?): 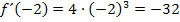
Die Tangente an 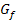 im Punkt P(-2|?) hat somit die Steigung -32.
im Punkt P(-2|?) hat somit die Steigung -32.
Nun gibt es auch die umgekehrte Fragestellung:Die Steigung einer Funktion  ist bekannt, aber der Punkt P auf der Funktion nicht.
ist bekannt, aber der Punkt P auf der Funktion nicht.

