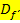a.) Unterschied zwischen Ableitung f´(x0) an einer bestimmten Stelle x0 und der Ableitungsfunktion f´(x)
Jeder Stelle x wird durch die Ableitungsfunktion  genau die Steigung von
genau die Steigung von  zugeordnet. (Erinnere dich an die Definition einer Funktion:Jedem x wird genau ein y zugeordnet. Die y-Koordinaten von
zugeordnet. (Erinnere dich an die Definition einer Funktion:Jedem x wird genau ein y zugeordnet. Die y-Koordinaten von  entsprechen dabei den Steigungen von
entsprechen dabei den Steigungen von  an den jeweiligen Stellen x.) Der Funktionswert
an den jeweiligen Stellen x.) Der Funktionswert  / das Ergebnis von
/ das Ergebnis von  entspricht also der Steigung von
entspricht also der Steigung von  an der Stelle x.
an der Stelle x.
Vielen Schulern fallt es anfangs schwer sich das vorzustellen.  ist einerseits die Steigung von
ist einerseits die Steigung von  und andererseits eine eigene Funktion. Hm? Du musst dir das folgenderma?en denken:Der Graph der Funktion
und andererseits eine eigene Funktion. Hm? Du musst dir das folgenderma?en denken:Der Graph der Funktion  ist eine Kurve und keine Gerade, daher hat die Funktion
ist eine Kurve und keine Gerade, daher hat die Funktion  an verschiedenen Stellen auch in der Regel unterschiedliche Steigungen. Die Steigung von
an verschiedenen Stellen auch in der Regel unterschiedliche Steigungen. Die Steigung von  hangt also von der jeweiligen Stelle x ab. Deshalb schreibt man jetzt auch nicht mehr m fur die Steigung, sondern
hangt also von der jeweiligen Stelle x ab. Deshalb schreibt man jetzt auch nicht mehr m fur die Steigung, sondern  . (Nur die Steigung von Geraden wird weiterhin mit m bezeichnet. Die Steigung einer Gerade ist im Gegensatz zur Steigung einer Kurve eine feste Zahl;die Steigung einer Gerade andert sich nicht, egal an welcher Stelle man sich auf der Gerade befindet.) Stelle dir nun Folgendes vor:Man hat den Graph
. (Nur die Steigung von Geraden wird weiterhin mit m bezeichnet. Die Steigung einer Gerade ist im Gegensatz zur Steigung einer Kurve eine feste Zahl;die Steigung einer Gerade andert sich nicht, egal an welcher Stelle man sich auf der Gerade befindet.) Stelle dir nun Folgendes vor:Man hat den Graph 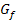 einer Funktion
einer Funktion  vor sich. An verschiedenen Stellen x werden die Tangenten an den Graph
vor sich. An verschiedenen Stellen x werden die Tangenten an den Graph 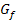 gelegt. Die Steigungen der verschiedenen Tangenten werden alle entweder mit dem Differenzialquotienten berechnet oder aus der Zeichnung abgelesen. Fasst man diese Tangentensteigungen nun als die y-Koordinaten einer neuen Funktion auf, kommt man zur Ableitungsfunktion
gelegt. Die Steigungen der verschiedenen Tangenten werden alle entweder mit dem Differenzialquotienten berechnet oder aus der Zeichnung abgelesen. Fasst man diese Tangentensteigungen nun als die y-Koordinaten einer neuen Funktion auf, kommt man zur Ableitungsfunktion  . Die x-Koordinaten der Punkte auf der Ableitungsfunktion entsprechen dabei immer den x-Koordinaten derjenigen Kurvenpunkte von
. Die x-Koordinaten der Punkte auf der Ableitungsfunktion entsprechen dabei immer den x-Koordinaten derjenigen Kurvenpunkte von 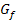 , in denen die jeweiligen Tangenten gezeichnet wurden, also den x-Koordinaten der Beruhrpunkte der Tangenten mit
, in denen die jeweiligen Tangenten gezeichnet wurden, also den x-Koordinaten der Beruhrpunkte der Tangenten mit 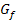 . Die Steigungen der Tangenten an den Graph
. Die Steigungen der Tangenten an den Graph 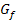 ergeben dann die y-Koordinaten der Punkte auf der Ableitungsfunktion.
ergeben dann die y-Koordinaten der Punkte auf der Ableitungsfunktion.
| Wir halten noch einmal fest:
Die Ableitung Die Tangentensteigung von Die Definitionsmenge Noch einmal in anderen Worten:In ihrem Differenzierbarkeitsbereich |

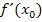 ist die Steigung einer Funktion
ist die Steigung einer Funktion 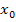 . Im Gegensatz dazu stellt die
. Im Gegensatz dazu stellt die 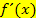
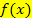
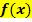
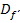 der Ableitungsfunktion wird als Differenzierbarkeitsbereich bezeichnet.
der Ableitungsfunktion wird als Differenzierbarkeitsbereich bezeichnet. 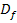 der Funktion
der Funktion