Rechnerischer Nachweis zu Bsp. 4
Rechnerischer Nachweis zu Bsp. 4,dafür dass sich beim Newton-Verfahren für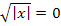 
mit beliebigen Startwerten 
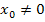eine alternierende Folge 
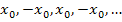ergibt
Die Gleichung 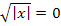entsteht bei der Berechnung der Nullstellen der Funktion 
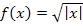. Wir schreiben sie betragsfrei und jeweils in Potenzschreibweise, um sie nachher ableiten zu können.
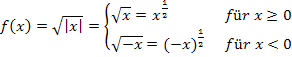
Nun bilden wir die Ableitung, da wir sie für das Newton-Verfahren benötigen.
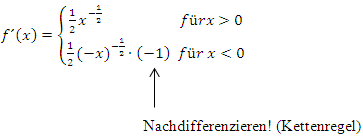
Hinweis:Beim Ableiten von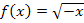 
muss die Kettenregel verwendet werden, wobei die innere Funktion hier –x ist. Zuerst wird die äußere Funktion, hier also die Wurzel abgeleitet;die innere Funktion bleibt dabei noch (statt x) stehen und wird erst nachdifferenziert. D.h. man muss noch mit der Ableitung der inneren Funktion multiplizieren. Die Ableitung von –x ist bekanntlich -1. Daher wird hier noch mit -1 multipliziert. Nähere Erläuterungen zur Kettenregel findest im Teil Weitere Ableitungsregeln.
Wir formen die Ableitung mit Hilfe des Potenzgesetzes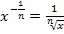 
um, damit sie etwas „schöner“ aussieht.
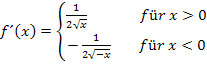
Nun legen wir fest, dass unser Startwert 
ein beliebiger positiver Wert ist. (Man kann entsprechend auch mit einem negativen Startwert beginnen. Wir müssen uns allerdings festlegen, damit wir wissen, mit welcher Ableitung wir beginnen müssen.) Nun geht es los mit dem Newton-Verfahren:
Hier noch einmal die Iterationsvorschrift: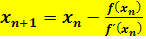 
mit n 
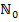
Mit n = 0 erhalten wir die Formel für den ersten Näherungswert 
.
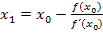
Da positiv ist, gilt: 
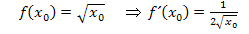
Das setzen wir in die Iterationsvorschrift ein und erhalten:
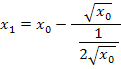
Den Ausdruck hinter dem Minuszeichen vereinfachen wir natürlich noch weiter. Den Hauptbruchstrich (längsten Bruchstrich) fassen wir dazu als normales Geteilt-Zeichen auf: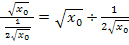 
Du weißt sicher:Man dividiert durch einen Bruch, indem man mit dem Kehrwert multipliziert. Daher gilt:
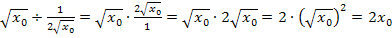
Damit ergibt sich für den ersten Näherungswert:
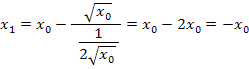
Es ist anzumerken, dass der ermittelte Wert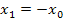 
hier, wie erwartet, kein Näherungswert für die einzige Lösung x = 0 der Gleichung 
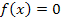darstellt. Wir haben aber auf jeden Fall gezeigt, dass für beliebige positive Startwerte gilt:
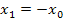
Für negative Startwerte ließe sich das Gleiche zeigen;wir sparen uns hier diesen Teil des Beweises. Du kannst das jedoch selbst einmal durchrechnen. Das wäre eine gute Übung für dich. Du musst für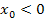 
allerdings mit 
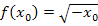und 
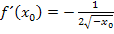arbeiten. Das Prinzip der Rechnung bleibt aber das Selbe.
Wir machen mit der Berechnung von 
weiter.
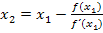
Mit 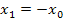ergibt sich:
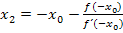
Da der Startwert positiv ist, muss der jetzt einzusetzende Wert 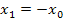entsprechend negativ sein. Für negative x gilt 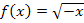und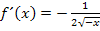 
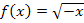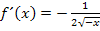. Daher müssen wir nun mit und arbeiten. Wir müssen dabei für x jeweils den Wert , also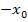 
einsetzen.
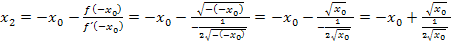
Wir vereinfachen den Doppelbruch wieder, indem wir mit dem Kehrbruch des Nenners multiplizieren. Dann lässt sich alles schön zusammenfassen.
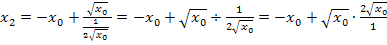
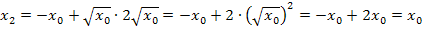
Nun haben wir gezeigt, dass sich für tatsächlich wieder der Startwert ergibt.
Nun könnten wir dies für die Werte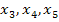 
immer so fortsetzen. Es würde sich ergeben:
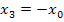
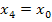
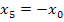
usw.
Das Gleiche müssten wir dann auch noch für den Fall 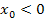machen. Das wäre allerdings vom Prinzip fast die gleiche Rechnung. Du dürftest das Grundprinzip jedoch inzwischen verstanden haben, so dass wir auf den Rest des Beweises verzichten wollen. Es ist hoffentlich klar geworden, dass sich tatsächlich bei der Gleichung 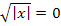für beliebige Startwerte (ungleich Null) durch das Newton-Verfahren eine Folge von „Näherungswerten“ der Form 
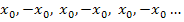ergibt. Eigentlich handelt es sich hierbei gar nicht um echte Näherungswerte für die Lösung der Gleichung 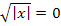, denn die einzige Lösung x = 0 kann damit überhaupt nicht, also auch nicht einmal näherungsweise berechnet werden. Das Newton-Verfahren versagt hier. (Eigentlich kann man die Gleichung sowieso ganz einfach nach x auflösen, so dass das Newton-Verfahren hier unnötig ist. Es sollte nur gezeigt werden, dass bei dieser Gleichung mit dem Newton-Verfahren keine Lösung gefunden werden kann, weil sich dabei immer wieder die gleichen Werte nur mit abwechselndem Vorzeichen ergeben.)
