Ausführliche Berechnung der Extrema zum 1. Bsp. (Newton-Verfahren)
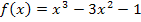
Die relativen Extrema von 
lassen sich leicht ermitteln. Man muss dazu nur 
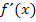bilden und gleich Null setzen. (Die Ableitung muss schließlich bei einem Extremum gleich Null sein, da die Tangente dort waagrecht verläuft und die Tangentensteigung, also 
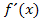, gleich Null ist.)
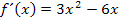
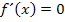
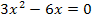
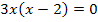
Ein Produkt ist gleich Null, wenn ein Faktor Null ist. Man kann daher die beiden Faktoren 3x und x – 2 einzeln gleich Null setzen.
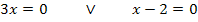
Die zugehörigen y-Koordinaten erhält man durch Einsetzen der berechneten x-Koordinaten in die Funktionsgleichung . Vorsicht:Nicht in die Ableitung 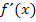einsetzen, wenn du die y-Koordinate eines Punktes von 
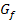berechnen willst; 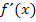ergibt schließlich die Steigung und nicht die y-Koordinate eines Punktes von .
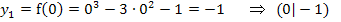
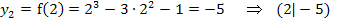
Eigentlich müsste man nun die Art der Extrema beispielsweise mit Hilfe des Monotonieverhaltens der Funktion oder, wenn du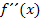 
schon gelernt hast, mit der zweitenAbleitung f´´(x)untersuchen. Wenn man aber sowieso zusätzlich eine Wertetabelle macht, ist aus dem Verlauf von 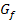sowieso klar, dass bei 
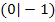ein relativer Hochpunkt und bei 
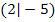ein relativer Tiefpunkt vorliegt. (Sogar ohne Wertetabelle kann man das in diesem Fall an Hand der y-Koordinaten erkennen. Da es sich hier um eine stetige Funktion ohne Definitionslücken handelt, also um eine Funktion, deren Funktionsgraph keine Sprungstellen oder senkrechte Asymptoten hat, kann man sagen, dass der Punkt mit der kleineren y-Koordinate sicher der Tiefpunkt ist und derjenige Punkt mit der größeren y-Koordinate entsprechend der Hochpunkt ist. Ein Terrassenpunkt kann hier nicht vorliegen, da es sich sowohl bei 
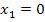als auch bei 
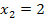um einfache Nullstellen der ersten Ableitung handelt. Ein Terrassenpunkt kann nur bei einer doppelten Nullstelle der Ableitung vorliegen.) Daher wissen wir:
