Das Newton-Verfahren
Bei der alternativen Form der Iterationsvorschrift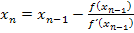 
beginnt der Index wegen n 
ℕ erst bei n = 1 und nicht wie bei der ersten Form bei n = 0. Dem entsprechend steht bei der alternativen Form der Iterationsvorschrift 
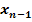für den zuletzt berechneten Näherungswert. Zu Beginn, also bei n = 1, entspricht dies dem Startwert 
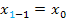. Mit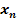 
ist dann bei 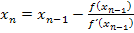der direkt nachfolgende Näherungswert, d.h. der als nächstes zu berechnende Wert gemeint.
Man beginnt bei 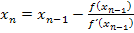mit n = 1;so ergibt sich wieder die schon oben gezeigte Formel für den ersten Näherungswert 
.
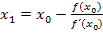Dann geht es weiter mit n = 2;so ergibt sich die oben schon gezeigte Formel für den zweiten Näherungswert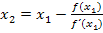 
.
Entsprechend wendet man die Iterationsvorschrift in gleicher Weise für n = 3, n = 4 usw. an, um die folgenden Näherungswerte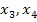 
usw. für die exakte Lösung a zu erhalten, bis man die gewünschte Genauigkeit erreicht hat. Du siehst, dass auch die zweite Iterationsvorschrift auf das Gleiche hinausläuft wie die erste. Die zu vollziehenden Rechenschritte sind jeweils dieselben.
Hier alle durchzuführenden Zwischenschritte beim Newton-Verfahren:
Näherungsweise zu lösende Gleichung: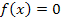 
Vorweg zu erledigen:
· Geeigneten Startwert 
wählen, falls nicht schon in der Aufgabe vorgegeben.
· Erste Ableitung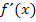 
bilden.
Berechnung des ersten Näherungswertes 
:
· 
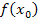bilden, d.h. den Startwert in 
einsetzen.
· 
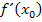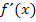bilden, d.h. den Startwert in die erste Ableitung einsetzen.
· Quotient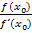 
berechnen, d.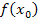h. durch 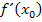dividieren.
· 
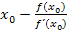berechnen, d.h. das Ergebnis des Quotienten 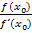von subtrahieren.
Dies ergibt den ersten Näherungswert . (Mit diesem Wert im Folgenden wieder genauso verfahren wie soeben mit dem Startwert , um den nächsten Näherungswert zu ermitteln.)
Ab jetzt wiederholen sich die einzelnen Rechenschritte immer wieder;allerdings verwendet man dann das jeweils letzte Ergebnis zum Weiterrechnen. Genau geht das folgendermaßen:
Berechnung des zweiten Näherungswertes 
:
· 
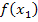bilden, d.h. den ersten Näherungswert in einsetzen.
· 
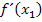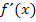bilden, d.h. den Näherungswert in die erste Ableitung einsetzen.
· Quotient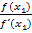 
berechnen, d.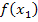h. durch 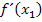dividieren.
· 
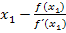berechnen, d.h. das Ergebnis des Quotienten 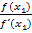von subtrahieren.
Dies ergibt den zweiten Näherungswert .
