Das Newton-Verfahren
Du fragst dich vermutlich, wieso diese allgemeine Formel des Newton-Verfahrens überhaupt gilt und wie man darauf gekommen ist. Also schauen wir uns doch gleich einmal die Herleitung an;sie ist auch gar nicht so schwierig.
Herleitung der Iterationsformel
Die Iterationsformel des Newtonverfahrens kann an Hand der folgenden Zeichnung ganz leicht hergeleitet werden.
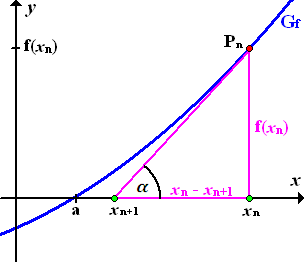
Abb.:Zur Herleitung der Iterationsformel des Newton-Verfahrens
Von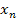 
, dem zuletzt berechneten Näherungswert für die gesuchte Nullstelle a der Funktion 
, geht man hoch zum Graphen 
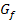zu dem Kurvenpunkt 
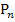. Dieser Punkt hat die Koordinaten 
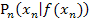. In 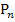wird die Tangente an 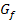eingezeichnet. Die Nullstelle dieser Tangente ergibt den nächsten Näherungswert 
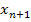. Durch die Punkte 
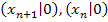und 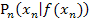ist ein rechtwinkliges Dreieck festgelegt. (In der Abbildung oben rosa eingezeichnet.) Seine Katheten haben die Längen 
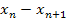und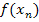 
. Des Weiteren ist der Winkel 
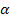eingezeichnet. Wie du hoffentlich weißt, gilt im rechtwinkligen Dreieck die Formel 
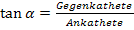. Bezüglich des Winkels 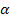ist 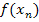die Gegenkathete und 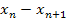die Ankathete. 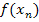liegt schließlich gegenüber von 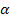und 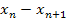liegt direkt an 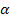d´ran. Somit gilt hier: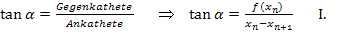 
Der Winkel 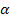ist der Schnittwinkel zwischen eingezeichneter Tangente und x-Achse, also der sogenannte Neigungswinkel der Tangente. Für den Neigungswinkel 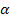einer Geraden gilt die Formel 
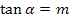. Dabei steht m für die Steigung der Geraden. In unserem Fall ist die Gerade die Tangente an 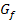im Kurvenpunkt 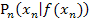. Ihre Steigung m kann mit der ersten Ableitung der Funktion an der Stelle 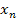berechnet werden: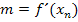 
Daher gilt: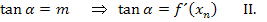 
In den Formeln I. und II. steht jeweils auf der linken Seite der Ausdruck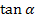 
. Daher können wir die Ausdrücke, die jeweils auf der rechten Seite von I. bzw. II. stehen, gleich setzen:
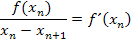
Wenn man diese Gleichung nach 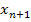auflöst, erhält man die Iterationsvorschrift des Newton-Verfahrens.
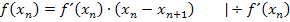
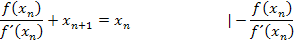
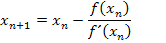
Das ist genau die bereits weiter oben gezeigte Iterationsvorschrift des Newton-Verfahrens. Nun müsste dir klar sein, warum diese Formel stimmt.
Alternative Schreibweise der Iterationsvorschrift
In manchen Büchern bzw. von manchen Lehrern wird auch die folgende Schreibweise der Iterationsvorschrift des Newton-Verfahrens verwendet:
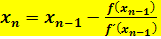mit n 
ℕ
Im Prinzip bedeuten beide gezeigten Iterationsvorschriften das Gleiche;sie unterscheiden sich allerdings in der Schreibweise der Indices (das sind die kleinen, tiefer gestellten „Zahlen“).
Bei der zuerst gezeigten Form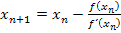 
gilt für den Index n 
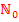;der Index n durchläuft dabei also alle natürlichen Zahlen einschließlich der Zahl Null.
