Das Newton-Verfahren
Man muss also zuerst den ersten Näherungswert 
berechnen. Mit rechnet man dann weiter, um damit den Wert 
zu ermitteln. Mit wird dann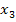 
berechnet und mit 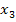dann wieder 
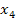. Man kann also keinen Schritt überspringen, sondern es müssen die Näherungswerte 
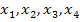… der Reihe nach berechnet werden, so lange bis die gewünschte Genauigkeit erreicht ist. Wenn sich nach einigen Schritten an der entsprechenden Nachkommastelle keine Veränderung mehr ergibt, kann man aufhören. Wenn man beispielsweise eine Genauigkeit von 4 Dezimalen erreichen soll, rechnet man solange, bis man auch die fünfte Nachkommastelle des gesuchten Wertes kennt, damit man weiß, ob man an der vierten Nachkommastelle auf- oder abrunden muss. Man muss für eine Genauigkeit von 4 Dezimalen also solange rechnen, bis sich von der ersten bis einschließlich der fünften Nachkommastelle von einem zum nächsten Näherungswert nichts mehr verändert.
Die oben gezeigten Formeln lassen sich allerdings noch zu einer einzigen Formel zusammenfassen. Dies ist die allgemeine Iterationsvorschrift des Newton-Verfahrens:
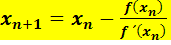
mit n 
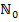(d.h. der Startwert wird mit 
bezeichnet, wie oben.)
Der Index n durchläuft dabei alle natürlichen Zahlen beginnend bei n = 0. Mit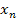 
ist jeweils der gerade berechnete Näherungswert gemeint bzw. zu Beginn, also für n = 0, der Startwert . Mit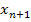 
ist der jeweils folgende Näherungswert gemeint.
Man beginnt also mit n = 0 und erhält dadurch die oben gezeigte Formel für den ersten Näherungswert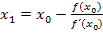 
.
Dann geht es weiter mit n = 1;so ergibt sich die oben schon gezeigte Formel für den zweiten Näherungswert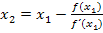 
.
Entsprechend wendet man die Iterationsvorschrift für n = 2, n = 3 usw. an, um die folgenden Näherungswerte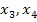 
usw. für die exakte Lösung a zu erhalten, bis man die gewünschte Genauigkeit erreicht hat. In den meisten Aufgaben müssen nicht mehr als zwei oder drei Schritte gemacht werden, denn es soll schließlich nur geprüft werden, ob du das Prinzip verstanden hast. Wer die ersten zwei Näherungswerte richtig berechnen kann, kann das auch bei den nachfolgenden. (Außer dass man sich vielleicht einmal auf dem Taschenrechner vertippt.) Es werden in Prüfungen und auch im Abi nie allzu viele Schritte verlangt. Das Ganze ist ohne programmierbaren Taschenrechner nämlich ganz schön viel Tipparbeit. Mit einem Computer oder mit einem programmierbaren Taschenrechner ist das Newton-Verfahren dagegen sehr schnell durchgeführt. Man braucht nur einmal einen entsprechenden Algorithmus (eine Rechenanweisung) programmieren und schon berechnet der Computer bzw. Taschenrechner den Wert so genau, wie man ihn braucht.
