Das Newton-Verfahren
Das macht man nun immer wieder, bis eine Näherung mit der gewünschten Genauigkeit erreicht ist. Der Punkt 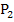 ist der Abbildung oben noch dargestellt, jedoch nicht mehr die zugehörige Tangente
ist der Abbildung oben noch dargestellt, jedoch nicht mehr die zugehörige Tangente 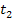 und der dritte Näherungswert
und der dritte Näherungswert 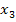 . Der Punkt
. Der Punkt 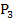 , die Tangente
, die Tangente 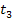 und der vierte Näherungswert
und der vierte Näherungswert 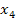 sind ebenfalls nicht mehr in der Abbildung dargestellt. Es ist einfach kein Platz mehr in der Zeichnung und das Prinzip hast du bestimmt längst verstanden.
sind ebenfalls nicht mehr in der Abbildung dargestellt. Es ist einfach kein Platz mehr in der Zeichnung und das Prinzip hast du bestimmt längst verstanden.
Nun denkst du dir wahrscheinlich:„O Gott! Wenn ich das alles ausrechnen muss, da werde ich ja alt und grau! Erst einmal die y-Koordinate des Punktes 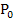 ausrechnen, dann in
ausrechnen, dann in 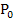 die Tangentengleichung aufstellen und die Nullstelle der Tangente, also die erste Näherung
die Tangentengleichung aufstellen und die Nullstelle der Tangente, also die erste Näherung  , ausrechnen. Dann als nächstes die y-Koordinate von
, ausrechnen. Dann als nächstes die y-Koordinate von 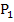 ausrechnen, dann im Punkt
ausrechnen, dann im Punkt 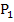 die Tangentengleichung aufstellen und die Nullstelle dieser Tangente, also
die Tangentengleichung aufstellen und die Nullstelle dieser Tangente, also  ausrechnen. Und, und, und…“ Keine Sorge, das musst du gar nicht! Erfreulicherweise gibt es eine Formel, mit deren Hilfe man direkt von
ausrechnen. Und, und, und…“ Keine Sorge, das musst du gar nicht! Erfreulicherweise gibt es eine Formel, mit deren Hilfe man direkt von  zu
zu  kommt und dann wieder direkt von
kommt und dann wieder direkt von  zu
zu  , entsprechend von
, entsprechend von  zu
zu 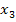 und immer so weiter. Diese Formel ist die oben bereits erwähnte Iterationsvorschrift.
und immer so weiter. Diese Formel ist die oben bereits erwähnte Iterationsvorschrift.
Iterationsvorschrift des Newton-Verfahrens:
Eine Iterationsvorschrift ist, wie gesagt, eine Rechenanweisung, die nacheinander immer wieder in gleicher Art und Weise angewendet wird. Man geht vom Startwert  aus, der schon möglichst nah an der gesuchten Lösung der Gleichung
aus, der schon möglichst nah an der gesuchten Lösung der Gleichung 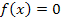 liegen sollte. Wenn der Startwert nicht in der Aufgabenstellung vorgegeben ist, entnimmt man ihn am besten einer Skizze oder man erstellt eine Wertetabelle für die Funktion
liegen sollte. Wenn der Startwert nicht in der Aufgabenstellung vorgegeben ist, entnimmt man ihn am besten einer Skizze oder man erstellt eine Wertetabelle für die Funktion 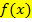 und schaut, zwischen welchen zwei x-Koordinaten der y-Wert sein Vorzeichen ändert. Zwischen diesen beiden x-Koordinaten muss die gesuchte Nullstelle liegen. Man nimmt dann diejenige der beiden x-Koordinaten, deren y-Koordinate weniger von Null abweicht. (Auf die Wahl eines geeigneten Startwertes werden wir weiter unten noch wesentlich genauer eingehen.)
und schaut, zwischen welchen zwei x-Koordinaten der y-Wert sein Vorzeichen ändert. Zwischen diesen beiden x-Koordinaten muss die gesuchte Nullstelle liegen. Man nimmt dann diejenige der beiden x-Koordinaten, deren y-Koordinate weniger von Null abweicht. (Auf die Wahl eines geeigneten Startwertes werden wir weiter unten noch wesentlich genauer eingehen.)
Den ersten Näherungswert  erhält man mit der Formel:
erhält man mit der Formel:![]()
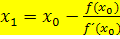
Den zweiten Näherungswert  erhält man mit der Formel:
erhält man mit der Formel:![]()
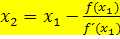
Den dritten Näherungswert 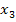 erhält man mit der Formel:
erhält man mit der Formel:![]()
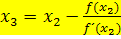
Wie man auf den vierten Näherungswert 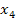 kommt, kannst du dir nun bestimmt schon selbst denken. Überlege dir erst selbstständig, wie die Formel für
kommt, kannst du dir nun bestimmt schon selbst denken. Überlege dir erst selbstständig, wie die Formel für 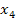 aussehen muss, bevor du weiterliest.
aussehen muss, bevor du weiterliest.
Hast du es dir alleine überlegt?
Dann bist du bestimmt darauf gekommen, dass sich der vierte Näherungswert 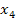 folgendermaßen bestimmen lässt:
folgendermaßen bestimmen lässt:![]()
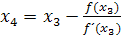
Das Prinzip hast du nun hoffentlich verstanden.

