Das Newton-Verfahren
Dabei gehen wir folgendermaßen vor:
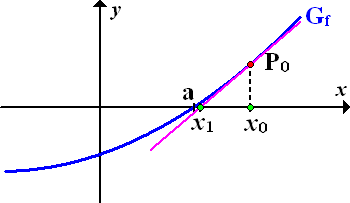
Wir entnehmen der Zeichnung einen Wert, der in der Nähe von a liegt. Dies ist unser Startwert 
. (Vergleiche nachfolgende Abbildung!) Von aus gehen wir senkrecht nach oben zum Funktionsgraph, also zu dem Kurvenpunkt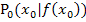 
;dort legen wir eine erste Tangente an den Funktionsgraphen 
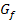. Wir bezeichnen diese Tangente hier mit 
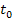. Als nächstes schneiden wir die Tangente 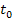mit der x-Achse;wir ermitteln also ihre Nullstelle. Die Nullstelle der Tangente ergibt den ersten Näherungswert 
.
Der Näherungswert liegt schon ziemlich nah an der exakten Lösung a. Wir wollen aber nachher einen noch besseren Näherungswert 
ermitteln. Deshalb hier noch eine stärkere Vergrößerung der Abbildung:
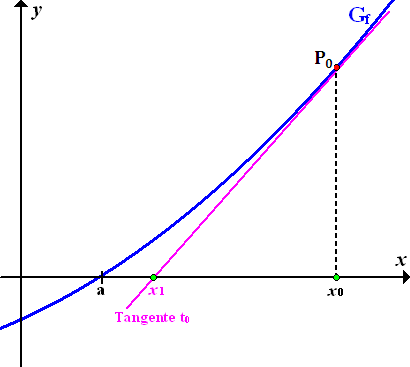
Wurde ein geeigneter Startwert gewählt, dann liegt der Wert näher an der exakten Lösung a, so wie hier in der Abbildung dargestellt. (Leider kann es auch passieren, dass der Wert weiter weg liegt von a als der Startwert . Das wäre sehr schlecht, dann hätte man nämlich einen ungeeigneten Startwert erwischt. In diesem Fall müsste man einen anderen Startwert verwenden, denn wir wollen uns schließlich immer mehr an a annähern und nicht immer weiter davon weggehen.)
Im Folgenden sei vorausgesetzt, dass eine bessere Näherung für a darstellt als der Startwert . In anderen Worten: soll näher an a liegen als . Wir gehen dann von wieder senkrecht nach oben zum Funktionsgraph. Den Kurvenpunkt, auf den wir so stoßen, bezeichnen wir mit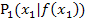 
. In diesem Punkt 
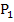wird nun wiederum eine Tangente an 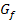gelegt. Wir nennen diese zweite Tangente 
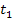. Wo die Tangente 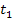die x-Achse schneidet, liegt der Wert . Die Nullstelle der zweiten Tangente entspricht also dem zweiten Näherungswert . Der Wert liegt noch etwas näher an a als unser erster Näherungswert und stellt somit eine noch bessere Näherung für a dar als .
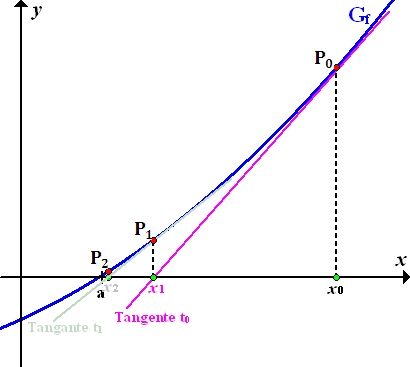
Abb.:Graph 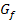mit Nullstelle a und den Näherungswerten für die Nullstelle 
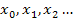aus dem Newton-Verfahren, dabei ergeben sich immer bessere Näherungen für a: liegt näher an a als und liegt wiederum näher an a als .
Nun kann man entsprechend immer so weiter machen, d.h. man geht von aus zum Kurvenpunkt 
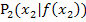und legt dort wieder eine Tangente an 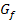. Wo diese Tangente die x-Achse schneidet, liegt der dritte Näherungswert 
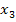. Von 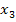geht man wieder zum zugehörigen Kurvenpunkt 
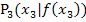und zeichnet dort die Tangente an 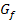. Die Nullstelle dieser Tangente entspricht dem vierten Näherungswert 
.
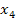