Das Newton-Verfahren
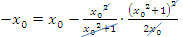
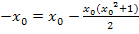
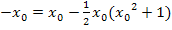
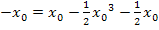
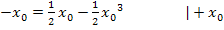
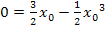
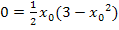
Durch das Ausklammern von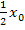 
im letzten Schritt, entstand ein Produkt gleich Null. Wie du sicher weißt, ist ein Produkt gleich Null, wenn einer der beiden Faktoren gleich Null ist. Daher können wir 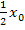und 
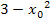einzeln gleich Null setzen. Die drei verschiedenen Lösungen werden im Folgenden mit 
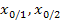und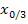 
bezeichnet.
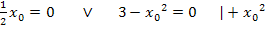
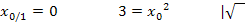
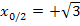
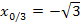
In der Aufgabe ist nach den von Null verschiedenen Startwerten gefragt, die beim Newton-Verfahren zu der alternierenden Folge der Form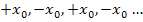 
führen. D.h. der Wert 
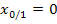kommt nicht in Frage. Es bleiben die beiden anderen Lösungen 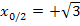und .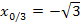
Verwendet man also entwe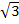der 
oder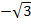 
als Startwert, ergibt sich bei der Funktion 
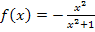durch das Newton-Verfahren keine Lösung der Gleichung 
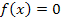, sondern stattdessen die alternierende Zahlfolge 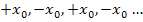. Das bedeutet, dass die Startwerte 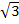und 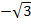absolut ungeeignet sind.
Anmerkung:An sich macht es natürlich sowieso keinen Sinn bei der Gleichung 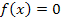mit 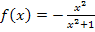das Newton-Verfahren anzuwenden. Die Lösung der Gleichung 
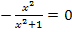liesse sich schließlich ganz leicht exakt ermitteln. Man müsste dazu erst mit dem Nenner multiplizieren. Dann entsteht nämlich eine ganz einfach zu lösende Gleichung:
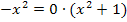
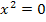
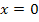
Somit ist 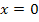die einzige Lösung der Gleichung .
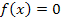Die Gleichung lässt sich also leicht nach x auflösen. Das Newton-Verfahren würde man bei dieser Gleichung daher überhaupt nicht benötigen. Die Aufgabe sollte bloßverdeutlichen, dass es bei manchen Gleichungen der Form 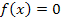vereinzelte Startwerte gibt, die absolut ungeeignet sind, da man in eine Art Endlosschleife gerät. Die berechneten Werte nähern sich nicht an die gesuchte Lösung an, sondern springen quasi immer wieder zwischen den Werten 
und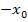 
hin und her, wenn man genau einen solchen Startwert erwischt. Sollte dir das einmal passieren, hilft nur eines:Neuen Startwert wählen und alles noch einmal von vorne! Doch keine Sorge, dass tritt nur extrem selten auf.
Dies soll uns hier an Beispielen zum Newton-Verfahren reichen. Das Rechenprinzip des Newton-Verfahrens ist dir inzwischen hoffentlich klar geworden.
Zusammenfassung:
Die Lösung(en) von Gleichungen, die sich auf anderem Wege nicht lösen lassen, kannst du mit Hilfe des Newton-Verfahrens zumindest näherungsweise berechnen. Dazu musst du die Gleichung auf die Form 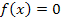bringen, also nach Null umstellen, und dann einen geeigneten Startwert wählen, falls er nicht schon in der Aufgabe angegeben ist.
