Das Newton-Verfahren
Der Wert 
unterscheidet sich nur im Vorzeichen vom Startwert 
. Allgemein kann man deshalb schreiben: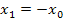 
Von gehen wir in der Abbildung wieder hoch zu dem Kurvenpunkt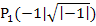 
, also zu dem Punkt 
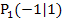. Legt man in diesem Punkt die Tangente 
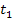an den Graphen und schneidet sie mit der x-Achse, stellt man fest, dass 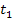die x-Achse wieder genau bei 
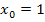schneidet. Der Schnittpunkt von 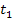mit der x-Achse ergibt normalerweise den zweiten Näherungswert 
der Gleichung 
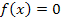. Der Näherungswert fällt hier aber genau mit dem Startwert zusammen. Es gilt hier also: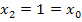 
Wenn man nun die nächste Tangente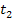 
zeichnen will, stellt man fest, dass diese wiederum mit der Tangente 
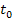zusammenfällt, welche die x-Achse bei 
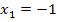schneidet. Die Tangente 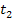schneidet normalerweise die x-Achse im dritten Näherungswert 
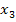, was hier allerdings mit 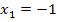identisch ist: 
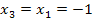Allgemein können wir wegen 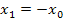schreiben: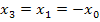 
So geht das nun ewig weiter. Alle weiteren Näherungswerte springen praktisch immer zwischen 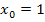und 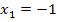hin und her. Wir drehen uns somit im Kreis. Eine echte Annäherung an die tatsächliche Nullstelle x = 0 findet nicht statt. Das Newton-Verfahren versagt.
Hier noch einmal die Ergebnisse des Newton-Verfahrens zu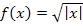 
in unserem konkreten Beispiel mit dem Startwert 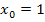übersichtlich zusammengefasst:
| Startwert |  |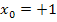
| 1. Näherung |  |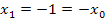
| 2. Näherung |  |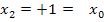
| 3. Näherung |  |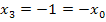
| 4. Näherung |  |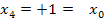
| 5. Näherung |  |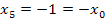
| usw. |
Die Werte springen also immer zwischen den Zahlen +1 und -1 hin und her. Man sagt:Sie bilden eine alternierende Folge der Zahlen +1 und -1, allgemein und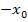 
. („Alternierend“ bedeutet dabei „vom Vorzeichen her abwechselnd“.)
Wir haben hier als konkretes Beispiel den Startwert 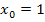verwendet. Mit jedem beliebigen anderen Startwert 
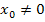würden wir auf das gleiche Problem stoßen. Das Newton-Verfahren liefert bei 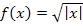immer Werte, die zwischen und 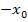hin und her springen, sich aber nie an die tatsächliche Nullstelle x = 0 annähern.
Den rechnerischen Nachweis dieser Tatsache können wir erst erbringen, wenn wir die Funktion 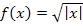ableiten können. Für 
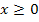ist dies kein Problem, denn hier gilt 
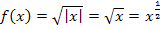. Es gilt für 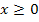somit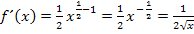 
. Für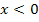 
gilt jedoch 
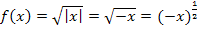. Um dies ableiten zu können, brauchen wir aber die sogenannte Kettenregel. Sie wird erst im Teil Weitere Ableitungsregeln erklärt. Deshalb verzichten wir momentan auf den rechnerischen Nachweis, dass das Newton-Verfahren bei 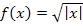für beliebige reelle Startwerte 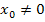versagt, weil es die Folge alternierender Zahlen und 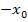liefert.
