Das Newton-Verfahren
Das liegt daran, dass bei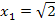 
die Tangente an 
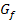waagrecht verläuft und somit die x-Achse nicht schneidet. Man könnte daher nicht mehr weiter rechnen.
Dieses Problem muss aber nicht immer gleich beim ersten Näherungswert 
auftreten;manchmal ergibt sich diese Problematik erst bei einem der späteren Näherungswerte. Das hängt bei der jeweiligen Gleichung 
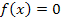von der Funktion 
und vom gewählten Startwert 
ab.
Empfehlenswert ist es daher grundsätzlich, sich immer vorweg mit Hilfe einer Skizze von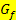 
einen Überblick über den groben Verlauf der jeweiligen Tangenten des Newton-Verfahrens zu verschaffen. Am Verlauf von 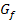wird am besten klar, welche Zahl als Startwert für das Newton-Verfahren vermutlich geeignet ist.
Verläuft der Funktionsgraph 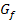in der Umgebung des gewählten Startwertes zwar nicht waagrecht, aber sehr flach und vielleicht auch noch sehr stark gekrümmt, könntest du zwar einen Wert für berechnen, doch liegt dieser Wert nicht näher an der gesuchten Nullstelle a, sondern noch weiter weg als der Startwert . Dadurch ergibt sich also keine bessere, sondern eine schlechtere Näherung, was natürlich sinnlos wäre. Das kannst du auch an der folgenden Abbildung erkennen.
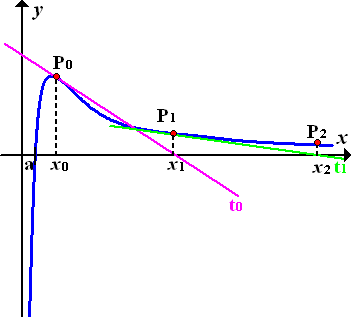
Abb.:Ungeeigneter Startwert , weil der Graph an der Stelle ziemlich flach und stark gekrümmt ist. Die Werte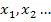 
liegen immer weiter entfernt vom gesuchten Wert a. Die Tangente 
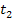im Punkt 
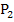ist nicht mehr eingezeichnet. Ihre Nullstelle 
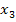liegt so weit rechts, dass sie schon gar nicht mehr in das gezeigte Koordinatensystem passt. Daher ist 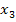nicht mehr eingezeichnet. Auch die Werte 
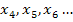sind nicht mehr eingezeichnet;sie würden noch weiter rechts liegen, d.h. sie würden sich immer weiter entfernen von der eigentlich gesuchten Nullstelle a.
In seltenen Fällen tritt ein weiteres Problem beim Newton-Verfahren auf:Die berechneten Näherungswerte können immer wieder zwischen zwei gleichen Zahlen hin und her springen. Zu einer wirklichen Annäherung an die gesuchte Nullstelle a kommt es daher nicht. Das Newton-Verfahren versagt dann natürlich. Das kann entweder direkt beim Startwert und dem ersten Näherungswert der Fall sein, dann erhält man eine Folge der Form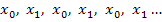 
, oder die beschriebene Problematik tritt erst bei einem der später berechneten Werte auf, zum Beispiel bei und 
. Dann ergibt sich eine Folge der Form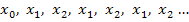 
Mache dir das beschriebene Problem an der nachfolgenden Abbildung klar!
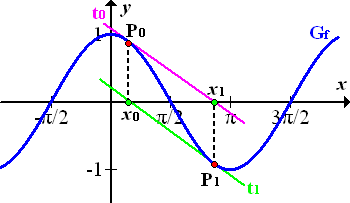
Abb.:Graph 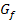der Funktion 
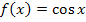mit den parallelen Tangenten 
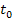an der Stelle und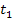 
beim ersten Näherungswert .
