Das Newton-Verfahren
Für alle Schüler eines bayerischen Gymnasiums (G8) und der mathematisch-technischen Zweige einer FOS oder BOS ist das Newton-Verfahren von enormer Wichtigkeit! Es wird mit größter Wahrscheinlichkeit in deiner Abiturprüfung eine Aufgabe dazu vorkommen. Da es an sich gar nicht schwer anzuwenden ist, sondern nur viel Tipparbeit mit dem Taschenrechner bedeutet, wären es verschenkte Punkte in der Abi-Prüfung, wenn du dich nicht damit beschäftigen würdest. Wie das Newton-Verfahren funktioniert, werden wir im Folgenden besprechen.
Grundprinzip des Newton-Verfahrens:
Wir haben eine Gleichung vor uns, die wir nicht auf „normalem“ Weg lösen können. Äquivalenzumformungen, also Auflösen nach x durch Umstellen der Gleichung, Mitternachtsformel oder auch Polynomdivision funktionieren nicht. Falls die Gleichung noch nicht nach Null aufgelöst vorliegt, musst du sie selbst jetzt gleich entsprechend umstellen. Auf einer Seite der Gleichung soll letztendlich auf jeden Fall nur die Zahl 0 stehen. Die andere Seite der Gleichung kann man dann als Funktion 
auffassen. Es liegt nun also eine Gleichung der Form 
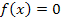vor.
Dass man mit dem Ansatz 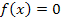die Nullstellen einer Funktion berechnet, ist dir sicherlich bekannt. Daher kann man die Lösungen unserer Gleichung auch als die Nullstellen der Funktion auffassen. Skizziert man nun den Graph der Funktion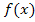 
zum Beispiel mit einer Wertetabelle, kann man die Nullstelle(n), soweit vorhanden, zumindest ungefähr aus der Zeichnung ablesen. (Es kann natürlich mehrere Lösungen und somit mehrere Nullstellen geben. Um jede dieser Lösungen jeweils näherungsweise zu berechnen, muss für jede Lösung / Nullstelle das Newton-Verfahren einzeln durchgeführt werden.) Stellen wir uns ´mal vor, der Graph von hätte genau eine Nullstelle, d.h. unsere Gleichung hätte genau eine Lösung. Wir nennen diese natürlich noch unbekannte Lösung im Folgenden a.
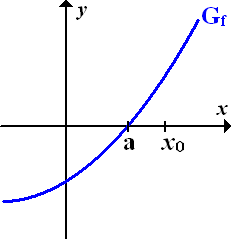
Abb.:Graph einer Funktion mit Nullstelle bei x = a und einem groben Näherungswert 
. Es handelt sich bei dieser Darstellung um eine extreme Vergrößerung des Verlaufs des Funktionsgraphen in der Umgebung der Nullstelle a. Es wirkt in dieser Abbildung daher so, als läge der Näherungswert ziemlich weit weg vom exakten Wert a. Dies ist aber nur auf den gewählten Maßstab zurückzuführen!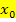 
liegt in Wirklichkeit ganz in der Nähe von a.
Die Nullstelle von liegt also genau an der Stelle x = a;entsprechend ist daher x = a die exakte Lösung der Gleichung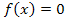 
und es gilt: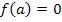 
Wir können a durch Rechnung nicht genau ermitteln, doch werden wir uns nun Schritt für Schritt immer mehr daran annähern.
