Das Newton-Verfahren

Wähle den Startwert einfach so, dass 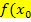) möglichst wenig von 0 abweicht, und dass der Graph an dieser Stelle nicht zu flach verläuft. Die zweite Ableitung 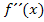, welche die Krümmung des Graphen beschreibt, lernt ihr dann in der Schule erst später.

Wie weiter oben bereits erwähnt, darf die Tangente an den Graph 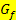an der Stelle 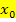keinesfalls waagrecht verlaufen, denn sonst kann sie die x-Achse gar nicht schneiden und es kann kein erster Näherungswert berechnet werden. Das ist extrem wichtig. Daher darfst du niemals als Startwert einen Punkt mit waagrechter Tangente, also ein Extremum oder einen Terrassenpunkt, verwenden. Vergleiche dazu auch die folgende Abbildung!

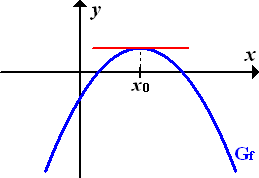
Abb.:Ungeeigneter Startwert mit waagrechter Tangente

Dass beim Startwert die Tangente nicht waagrecht liegen darf, siehst du auch an der Konvergenzbedingung:

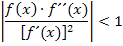
Bei einer waagrechten Tangente ist die Ableitung 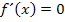, so dass der Nenner der Konvergenzbedingung gleich Null werden würde. Das Einsetzen von in die Iterationsvorschrift 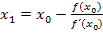wäre dann ebenfalls gar nicht möglich;der Nenner würde auch hier Null werden. Es könnte somit kein Näherungswert berechnet werden.

Genau genommen darf bei keinem der berechneten Näherungswerte die Tangente waagrecht verlaufen, denn sonst kann man nicht weiterrechnen! Der Nenner würde beim Versuch den nächsten Näherungswert auszurechnen Null ergeben. Mache dir dieses Problem an der nächsten Beispielaufgabe klar!

3. Bsp.:

In der nachfolgenden Abbildung ist der Graph der Funktion 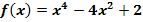dargestellt. Die Nullstellen der Funktion 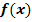können mit Hilfe der Substitution 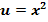und anschließender Verwendung der Mitternachtsformel exakt berechnet werden. Wenn man dennoch stattdessen versucht die Nullstelle, welche zwischen 0,5 und 1 liegt, mit dem Newton-Verfahren näherungsweise zu berechnen, könnte man einen Startwert 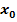erwischen, mit dem beim Newton-Verfahren das Problem auftritt, dass die Tangente in 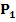waagrecht verläuft und sich daher alle weiteren Näherungswerte nicht berechnen lassen. Vergleiche Abbildung! Ermittle diesen ungeeigneten Startwert 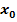für die Näherung der Nullstelle zwischen 0,5 und 1 der Funktion 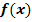auf 4 Dezimalen genau!

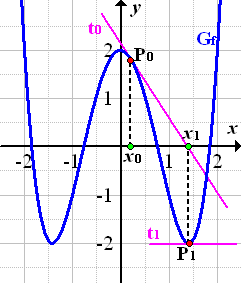
Abb.:Tangente 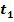an der Stelle 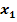waagrecht Berechnung von 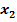und allen weiteren Näherungswerten unmöglich

Lösung:

Wenn bei der Funktion 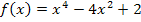mit dem Newton-Verfahren die Nullstelle zwischen 0,5 und 1 näherungsweise berechnet wird, könnte die Tangente 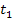beim ersten Näherungswert waagrecht verlaufen, so dass diese Tangente die x-Achse niemals schneidet. Dann ließen sich die weiteren Näherungswerte nicht berechnen.

---